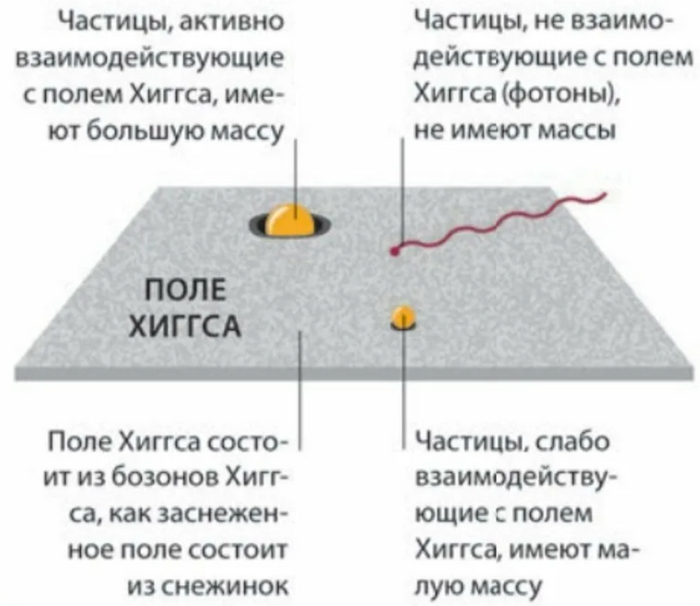
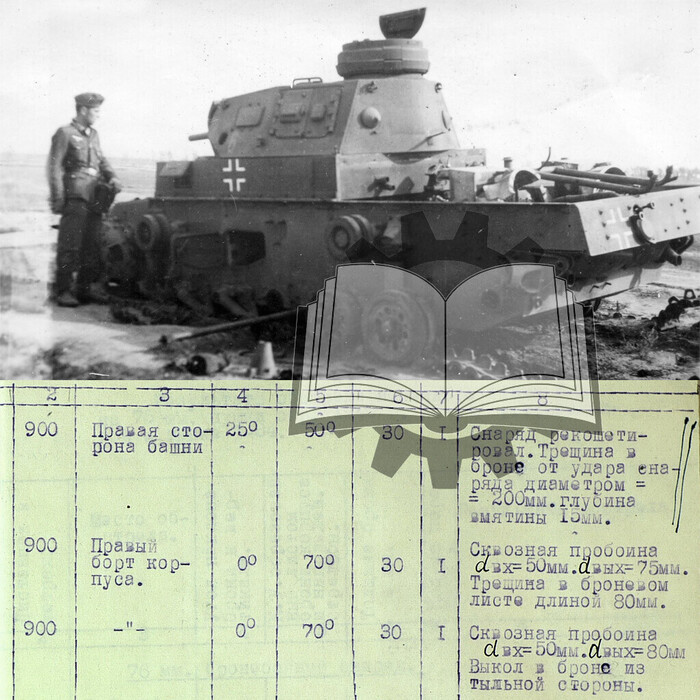
Наука и производство
Добро пожаловать в нашу энциклопедию техники, содержащий огромное количество терминов, статей, рефератов о технике и производстве, промышленности, транспорте, строительстве. У нас вы узнаете о развитии науки и техники, достижениях, также историю, философию, проблемы и культуру науки и техники. Некоторые её разделы посвящены промышленному развитию России.