При принятой номенклатуре запасных частей расчет их количества производится, исходя из условия поддержания работоспособного состояния РЭО и СА в течение установленного времени с вероятностью не ниже требуемой. В результате расчета оптимального количества запасных частей при минимальных затратах (объеме, массе или стоимости) на комплект ЗИП определяют время эксплуатации и вероятность обеспеченности или при заданных ограничениях по затратам (объеме, массе или стоимости) вычисляют максимальную вероятность обеспеченности.
Работоспособность РЭО и СА многократного действия зависит от количества запасных частей, поэтому необходимо определить количественную зависимость вероятности P (t) того, что система выполнит заданные функции за время t при наличии z запасных частей. Эта зависимость позволяет установить влияние количества запасных частей на надежность, а также определить необходимое число запасных элементов, обеспечивающих с вероятностью Pz{t) безотказную работу объекта.
При определении необходимого количества запасных частей часто используют такой критерий, как среднее время вынужденного простоя прибора из-за отсутствия в ЗИП необходимых элементов. Отсутствие в комплекте ЗИП запасного элемента, который мог бы заменить какой-либо отказавший в процессе эксплуатации элемент РЭО и СА, понимается как отказ комплекта ЗИП.
Пусть рассматриваемая система содержит ![]() элементов i-го типа (i= 1, 2, ... m), соединенных, исходя из требований надежности, последовательно. При экспоненциальном законе распределения для внезапных отказов при включенном (рабочий режим) и выключенном (режим ожидания) состоянии элементов РЭО и СА среднее ожидаемое количество отказов в течение заданного расчетного времени
элементов i-го типа (i= 1, 2, ... m), соединенных, исходя из требований надежности, последовательно. При экспоненциальном законе распределения для внезапных отказов при включенном (рабочий режим) и выключенном (режим ожидания) состоянии элементов РЭО и СА среднее ожидаемое количество отказов в течение заданного расчетного времени ![]() , будет равно:
, будет равно:
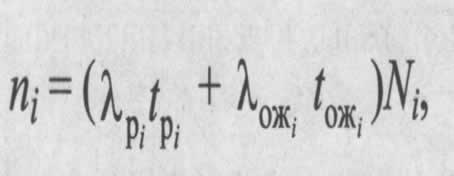
где ![]() - интенсивность отказов элементов i-гo типа в рабочем режиме и режиме ожидания (хранения);
- интенсивность отказов элементов i-гo типа в рабочем режиме и режиме ожидания (хранения); ![]() - время работы элемента i-ro типа и время ожидания.
- время работы элемента i-ro типа и время ожидания.
Если в электрической системе вместо отказавшего элемента каждый раз будет устанавливаться новый элемент из комплекта ЗИП (отказавший элемент не восстанавливается), то число израсходованных частей ![]() будет равно числу отказов п, возникших за это же время.
будет равно числу отказов п, возникших за это же время.

где ![]() - количество запасных частей i-гo типа.
- количество запасных частей i-гo типа.
Если в комплекте ЗИП нет ни одной запасной части ![]() , формула (8.1) соответствует вероятности безотказной работы системы из элементов i-ro типа, описываемой экспоненциальным законом:
, формула (8.1) соответствует вероятности безотказной работы системы из элементов i-ro типа, описываемой экспоненциальным законом:
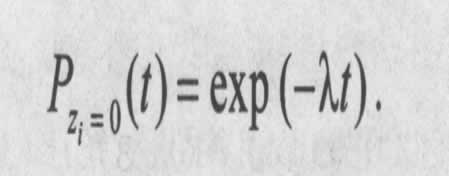
Вероятность того, что система из элементов i-го типа за время эксплуатации t выполнит свои функции, т. е. запасных частей i-гo типа будет достаточно, определится в виде суммы:
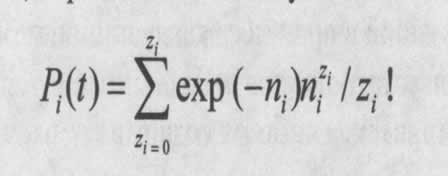
Функцию ![]() для определения необходимого количества запасных частей
для определения необходимого количества запасных частей ![]() данного типа в зависимости от
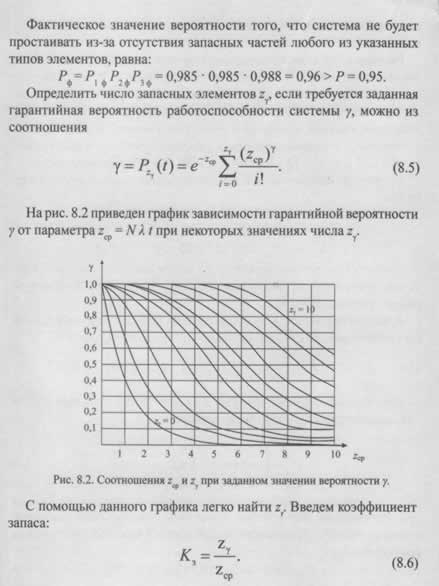
данного типа в зависимости от ![]() можно представить в виде номограммы (рис. 8.1).
можно представить в виде номограммы (рис. 8.1).
Из номограммы видно, что при количестве запасных частей ![]() равном ожидаемому количеству отказов
равном ожидаемому количеству отказов ![]() вероятность того, что электрическая система не будет простаивать из-за отсутствия запасных частей при n > 1, будет незначительно превышать 0,50, что явно недостаточно для нормальной работы системы. Это объясняется тем, что фактическое число отказов данных частей за расчетное время примерно с равной вероятностью может быть как меньше, так и больше среднего ожидаемого количества отказов
вероятность того, что электрическая система не будет простаивать из-за отсутствия запасных частей при n > 1, будет незначительно превышать 0,50, что явно недостаточно для нормальной работы системы. Это объясняется тем, что фактическое число отказов данных частей за расчетное время примерно с равной вероятностью может быть как меньше, так и больше среднего ожидаемого количества отказов ![]()
Вероятность достаточности запасных частей i-го типа в комплекте ЗИП рассчитывают, исходя из заданной величины вероятности ![]() того, что общего количества запасных частей всех типов в комплекте ЗИП будет достаточно для поддержания работоспособности системы. Для особо ответственных устройств заданные значения вероятности того, что система выполнит заданные функции за время t при наличии z
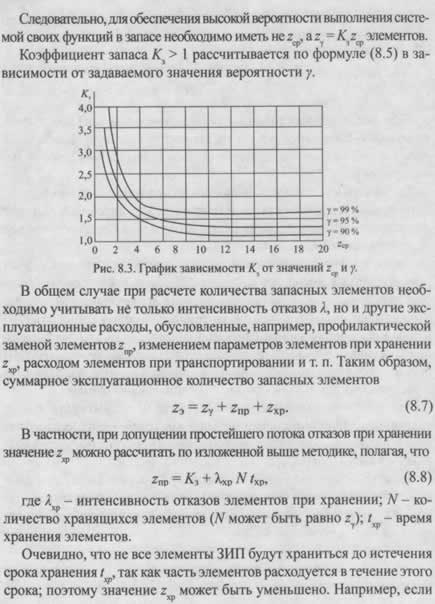
того, что общего количества запасных частей всех типов в комплекте ЗИП будет достаточно для поддержания работоспособности системы. Для особо ответственных устройств заданные значения вероятности того, что система выполнит заданные функции за время t при наличии z