Тестовое диагностирование предполагает подачу на вход ОД специальных тестовых воздействий. Для упрощения исследований непрерывных объектов используют типовые воздействия. Наиболее распространенным типовым воздействием является единичная ступенчатая функция, или единичный скачок (рис. 13.4).
Аналитически единичная ступенчатая функция записывается в виде:
![]()
Реакция ОД на это воздействие представляет переходную функцию h(t)
В качестве тестового воздействия может использоваться неединичная ступенчатая функция, называемая сигналом включения вида (рис. 13.5).
![]()
Этот сигнал достаточно просто реализуется подачей питания.

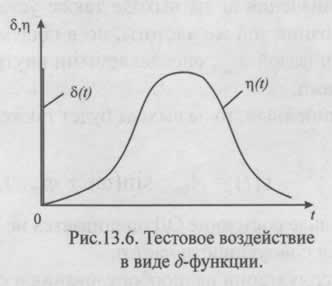
Зная реакцию исправного объекта на кратковременное включение в работу, можно оценить его техническое состояние.
Для исследования динамических режимов работы судового РЭО и СА широко используют так называемый частотный метод, при котором тестовым воздействием является синусоидальный сигнал.
Частотный метод позволяет с достаточной степенью точности оценить как устойчивость объекта, так и качество переходного процесса регулирования.
Основным понятием частотных методов исследования является понятие амплитудной-фазочастотной характеристики объекта в целом и ее отдельных звеньев (АФЧХ). В отличие от переходной характеристики АФЧХ получают путем подачи на вход объекта или отдельного динамического звена системы типового гармонического воздействия с постоянной амплитудой, но с переменной частотой, которая изменяется непрерывно в широком диапазоне:
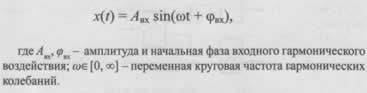

Дефект типа «Const 1» соответствует короткому замыканию на высокий потенциал, дефект типа «Const 0» - короткому замыканию на «О».
Функциональный метод основан на использовании математических моделей, определяющих функциональные зависимости между переменными, представляющими его входы и выходы. В качестве таких моделей могут быть таблицы функций неисправности (ТФН), строки которой соответствуют наборам входных воздействий, а столбцы -работоспособному и каждому неработоспособному состоянию ОД.
Для тестирования логических схем могут быть использованы как регулярные последовательности импульсов, так и псевдослучайные последовательности двоичных сигналов, которые легко реализуются с помощью регистра сдвига с сумматором по модулю 2 в цепи обратной связи, с периодом Тr= (2m -1) i, где m - число разрядов регистра, i - период следования запускающих импульсов.
При этом в зависимости от рассматриваемого интервала последовательность импульсов может рассматриваться как регулярная, случайная и псевдослучайная.
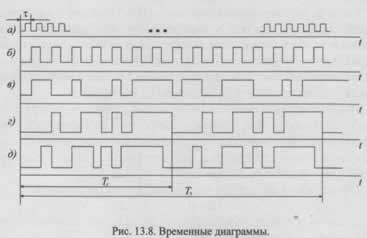
Для сравнения на рис. 13.8 представлены временные диаграммы регулярных, случайных и псевдослучайных сигналов, генерируемых четырехразрядным регистром сдвига с линейной обратной связью.
Регулярные сигналы (рис. 13.8,6), независимо от интервала времени, на котором они рассматриваются, обладают свойством периодичности.
На рис. 13.8, в представлен случайный сигнал.
Псевдослучайным сигналам в зависимости от рассматриваемого интервала времени присущи различные свойства: на интервале T1 Tr псевдослучайные сигналы рассматриваются как регулярные периодические сигналы (рис. 13.8, г, д).
Основной недостаток тестов в виде псевдослучайных последовательностей сигналов - отсутствие уверенности в стопроцентном срабатывании всех элементов проверяемой схемы.

