На просторах англоязычного Интернета я нашел еще одну вдохновляющую статью (по крайней мере, лично для меня). Как всегда, машинные переводы оставляют желать лучшего, поэтому я, как всегда, делюсь своим оригинальным переводом со всеми заинтересованными лицами. Оригинальный текст здесь. Приятного чтения!
В конце XIX века Карл Вейерштрасс изобрел фракталоподобную функцию, которая была осуждена математическим сообществом как «ужасное зло». Со временем это изменило основы математики.
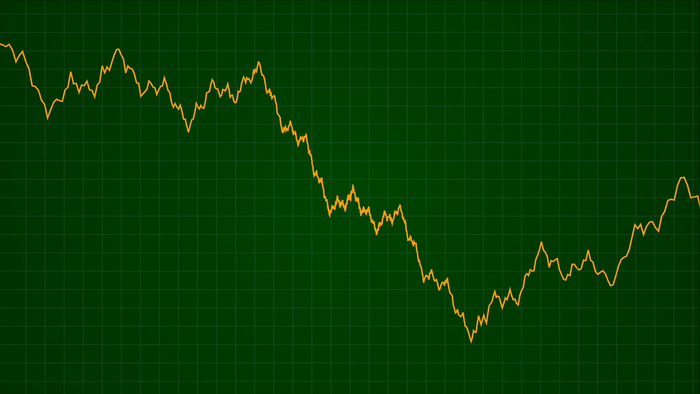
Если долго увеличивать этот график, функция Вейерштрасса будет становиться все более неровной и зубчатой.
Математический анализ — мощный математический инструмент. Однако за сотни лет, прошедшие с момента его изобретения в XVII веке, его фундамент пошатнулся. Его ключевые концепции порой основаны на интуиции и неформальных рассуждениях, а не на точных формальных определениях, общепринятых в математике.
По словам Майкла Барани, историка математики и науки, споры об исчислении привели к появлению двух различных школ мысли в развитии математики в XVIII и XIX веках. Французские математики в целом удовлетворены текущей ситуацией. Их больше интересовало применение исчисления к физическим проблемам — например, использование его для расчета траекторий планет или изучения поведения электрических токов. Однако в XIX веке немецкие математики начали подвергать сомнению устоявшиеся идеи. Они пытаются найти контрпримеры, которые разрушают устоявшиеся стереотипы и в конечном итоге ставят математический анализ на более устойчивую основу.
Одним из таких математиков был Карл Вейерштрасс. Несмотря на ранний талант Вейерштрасса к математике, отец заставил его изучать финансы, намереваясь поступить на прусскую государственную службу. Говорят, что Вейерштрассу было скучно на этих уроках, и он проводил большую часть времени за выпивкой и фехтованием; в конце 1830-х годов, несмотря на то, что он не получил ученой степени, он стал учителем средней школы, преподавая различные предметы, включая математику, физику, каллиграфию и гимнастику.

Карл Вейерштрасс начал свою математическую карьеру, когда ему было почти 40 лет. Его приверженность строгости и логике в конечном итоге привела к рождению современного математического анализа.
Вейерштрасс начал карьеру профессионального математика только в возрасте почти 40 лет. Но он изменил науку, показав миру своих математических «монстров".
Основы математического анализа
В 1872 году Вейерштрасс опубликовал функцию, которая бросила вызов всему, что математики ранее думали об исчислении. Однако публикация Вейерштрасса была встречена с равнодушием, гневом и страхом, особенно со стороны ведущих представителей французской математической школы. Анри Пуанкаре осудил деятельность Вейерштрасса как «оскорбление здравого смысла». Шарль Эрмит назвал это «отвратительным злом".
Чтобы понять, почему результаты Вейерштрасса вызвали столь шокирующую реакцию, необходимо сначала понять два самых основных понятия математического анализа: непрерывность и дифференцируемость.
Непрерывная функция — это именно то, что следует из ее названия: функция без разрывов и скачков. Вы можете провести линию от любой точки этой функции до любой другой точки, не отрывая карандаша.
Математический анализ в первую очередь занимается определением того, насколько быстро изменяются такие непрерывные функции. Грубо говоря, он работает путем аппроксимации заданной функции с помощью прямых, неперпендикулярных линий.
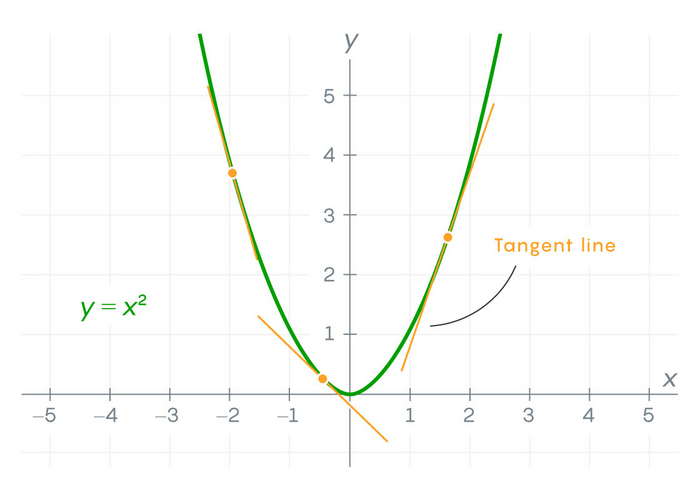
В любой точке этой кривой можно провести «касательную линию» — линию, которая наиболее точно приближается к кривой вблизи этой точки. Наклон или крутизна касательной измеряет скорость изменения функции в этой точке. Можно определить другую функцию, называемую производной, которая определяет наклон касательной в каждой точке исходной функции. Если производная существует во всех точках, то исходная функция называется дифференцируемой.
Функции, содержащие разрывы, никогда не являются дифференцируемыми: вы не можете провести касательную линию, приближающую разрыв, а это значит, что ваша производная там не существует. Но даже непрерывные функции не всегда дифференцируемы во всех точках. Рассмотрим функцию «абсолютного значения», которая выглядит следующим образом:
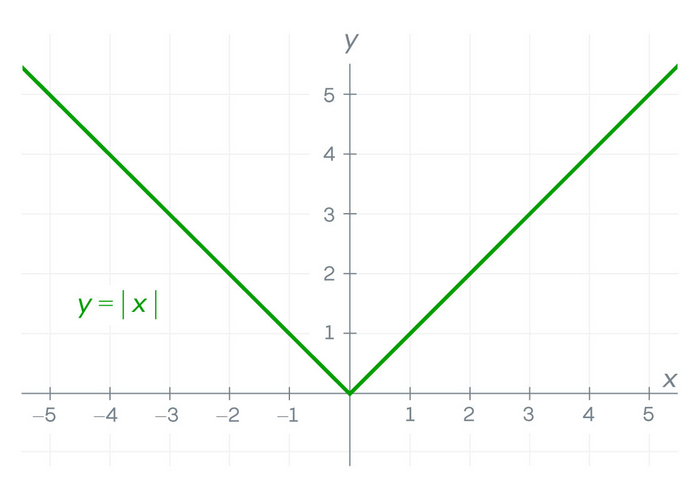
На левой стороне этой V-образной кривой касательная имеет отрицательный наклон. С правой стороны они имеют положительный наклон.
Обратите внимание: Нанороботы, вдохновленные человеком … будет создана сперма, которая исцелит наши тела.
На вершине нижнего холма направление склона резко меняется. Производная этой функции на данный момент не существует, хотя она хорошо определена в другом месте.Это не беспокоило большинство математиков XIX века. Они считали, что это изолированное явление: пока функция непрерывна, может быть лишь конечное число точек, в которых производная не определена. Во всех остальных точках функция должна оставаться плавной и непрерывной. Другими словами, функция может «прыгать» только в ограниченном диапазоне.
Фактически, в 1806 году известный французский математик и физик Андре-Мари Ампер утверждал, что доказал это. Его рассуждения остаются неизменными на протяжении десятилетий. Затем появился Вейерштрасс.
Чудовище Вейерштрасса
Вейерштрасс открыл функцию, которая, согласно доказательству Ампера, не могла существовать: она была непрерывна всюду, но не всюду дифференцируема.
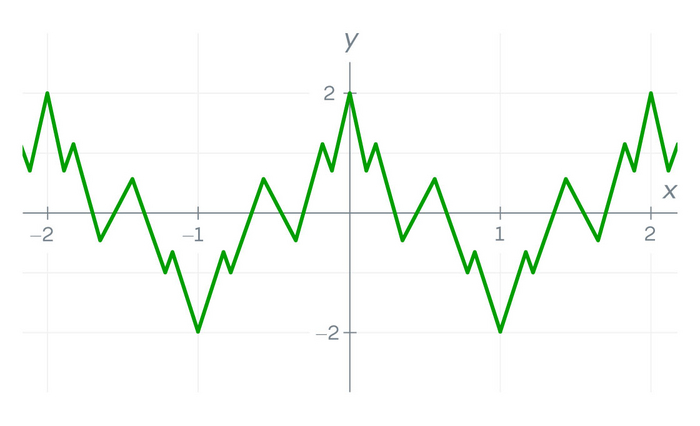
Он создал его, сложив бесконечное число волнообразных «косинусных» функций. Чем больше членов он добавлял, тем больше «скакала» его функция — пока в конце концов она не начала резко менять направление в каждой точке, как бесконечно зазубренная пила.
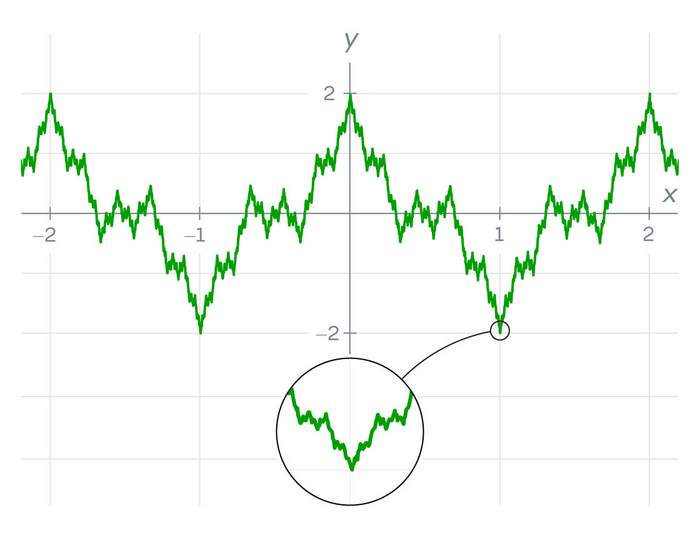
Многие математики отвергли эту функцию. По их словам, это аномалия, а работа Вейерштрасса была названа педантичной и бесполезной с математической точки зрения. Они даже представить себе не могли эту сцену. Во-первых, когда вы пытаетесь построить график функции Вейерштрасса, в некоторых областях он выглядит гладким. Только при увеличении масштаба вы замечаете, что эти области неровные, и с каждым увеличением масштаба они становятся все более неровными и «плохо» себя ведут («больные.
Но Вейерштрасс безупречно продемонстрировал, что, хотя его функция не имеет разрывов, она никогда не является дифференцируемой. Чтобы доказать это, он сначала пересмотрел определения «непрерывности» и «дифференцируемости», предложенные десятилетиями ранее математиками Огюстеном-Луи Коши и Бернаром Больцано. Эти определения основаны на неопределенных, упрощенных описаниях на естественном языке и непоследовательных обозначениях, поэтому их легко понять неправильно.
поэтому Вейерштрасс переписал их, используя точный язык и конкретные математические формулы. (Каждый студент-математик изучает определение предела в терминах эпсилон-дельта; Вейерштрасс ввел современную версию этого определения в качестве основы для определений непрерывности и дифференцируемости.)
Затем ему удалось показать, что его функция удовлетворяет более строгому определению непрерывности. В то же время он смог показать, что в любой точке его новое формальное определение производной функции никогда не будет иметь конечного значения; оно всегда будет «выходить за пределы» бесконечности. Другими словами, непрерывность не подразумевает дифференцируемость. Его функция была именно тем монстром, которого всегда боялись математики.
Доказательство показало, что математический анализ больше не может полагаться на геометрическую интуицию, как это делали его создатели. Он устанавливает новые стандарты в этой дисциплине, основанные на тщательном анализе уравнений. Математикам пришлось последовать примеру Вейерштрасса и еще больше усовершенствовать свои определения функций, свое понимание связей между непрерывностью и дифференцируемостью, а также свои методы вычисления производных и интегралов. Эта работа по стандартизации математического анализа впоследствии развилась в область математики, известную сегодня как исчисление (первоначально называвшуюся «исчислением бесконечно малых»); Вейерштрасс считается одним из ее основателей.
Однако влияние его возможностей выходит далеко за рамки основ самого математического анализа. Она показала, что математика полна монстров: кажущиеся невозможными функции, странные объекты (один из первых примеров фракталов), «дикое» поведение математических объектов. «Функция Вейерштрасса должна открыть вам глаза на бесчисленное множество возможностей, существующих во Вселенной», — сказал Филип Глейсман из Пенсильванского университета.
Оказывается, у этого есть много практических применений. В начале 20 века физики захотели изучить броуновское движение — хаотическое перемещение частиц в жидкости или газе. Поскольку это движение непрерывное, но не плавное (характеризуется быстрыми и бесконечно малыми колебаниями), функции типа Вейерштрасса хорошо подходят для моделирования этого явления. Аналогичным образом эти функции используются для моделирования неопределенности в процессе принятия решений и принятия рисков человеком, а также сложного поведения финансовых рынков.
Как и в случае с самим Вейерштрассом, значение математических функций и объектов порой раскрывалось спустя долгое время после их фактического открытия. Однако подобные «монстры» по-прежнему оказывают влияние на математику и ее практическое применение.
Мой проект по науке и философии
[Моя] Наука Исследования Ученый Популярная наука Математика Видео Без звука Короткое видео Длинный текст 35Больше интересных статей здесь: Новости науки и техники.
Источник статьи: Рваная, чудовищная функция, которая сломала математический анализ.
- Небо завалено радиочастотными помехами (РЧП), но благодаря двум астрономам, отследившим отраженный от пролетающего мимо самолета сигнал телепередачи, возможно, появился новый способ уничтожить некоторые из несанкционированных сигналов, которые досаждают н
- Астероид 2024 YR4, открытый в декабре 2024 года, в настоящее время находится под пристальным вниманием научного сообщества

