Если в результате отдельного испытания изучаемое событие А (отказ) может происходить с вероятностью р, а вероятность его непоявления q = 1 -р, то количество появлений события А в N независимых испытаниях (на N объектах) будет случайной величиной, подчиненной биноминальному закону распределения.
Согласно этому закону вероятность появления события А равна n раз при N испытаниях:
где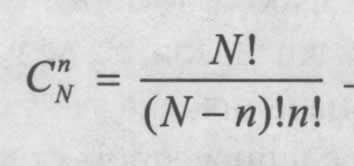 
- число различных сочетаний из N по n.
Математическое ожидание М(n), дисперсию и среднеквадратическое отклонение а числа n появлений события А находят по формулам:
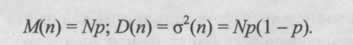
На практике часто требуется определить вероятность хотя бы одного появления события А при N испытаниях:
Закон распределения Пуассона. Распределение Пуассона играет особую роль в теории надежности, поскольку оно описывает закономерность появления случайных отказов в сложных системах. Поток случайных событий (поток отказов или восстановлений) есть последовательность таких событий, происходящих одно за другим. Поток событий называется пуассоновским, если он удовлетворяет требованиям стационарности, ординарности и отсутствия последствия.
Стационарность означает, что вероятность появления определенного числа событий (отказов) за данный промежуток времени не зависит от положения промежутка на оси времени, а зависит только от его длины. Для такого потока плотность появления постоянна во времени.
Ординарность - невозможность появления более одного события в один и тот же момент времени.
Отсутствие последствия показывает, что вероятность появления определенного числа событий в течение некоторого промежутка времени не зависит от числа и характера возникновения событий до начала этого промежутка.
