Для эффективного формализованного процесса диагностики необходимо создать модель объекта диагностирования (ОД). Эта модель подразумевает декомпозицию ОД на отдельные, функционально связанные элементы.
Диагностическая модель — это искусственный объект, который может замещать реальный в ходе исследований, предоставляя информацию, необходимую для проведения технического диагностирования.
Функциональные модели как основа диагностики
Чаще всего для радиоэлектронного оборудования (РЭО) в качестве диагностической модели применяется функциональная модель. Она наиболее точно отражает логику взаимодействия компонентов системы. Её можно построить на базе принципиальной или структурной схемы объекта, но ключевое отличие заключается в том, что разбиение на элементы определяется требуемой точностью локализации неисправностей. Функциональную модель также можно разработать, формализуя текстовые документы с использованием условных обозначений.Роль математического моделирования
Для создания алгоритмов и программ диагностики, изучения объектов, разработки средств диагностирования и оценки эффективности систем широко применяется математическое моделирование. Этот подход незаменим, когда прямое исследование характеристик реального объекта невозможно.Математическая модель ОД — это формальное описание объекта и его поведения в различных технических состояниях. Процесс её создания для сложного объекта включает три этапа:
1) Составление содержательного описания объекта;
2) Построение формализованной схемы;
3) Преобразование формализованной схемы в математическую модель.
Типы математических моделей в диагностике
В диагностике выделяют два основных типа математических моделей: неявные и явные.Неявная модель предполагает наличие лишь описания исправного объекта и набора правил, по которым можно вывести модели для любого неисправного состояния.
Явная модель, напротив, содержит не только описание исправного объекта, но и явные описания каждой его возможной неисправной модификации. Такая модель часто строится в виде набора элементарных проверок и их результатов. Элементарная проверка — это неделимая часть процесса диагностики, характеризующаяся тестовым (или рабочим) воздействием на объект и снимаемым с него ответом. Результат R элементарной проверки в общем виде можно представить как функцию состояния объекта и воздействия.

Таблица функций неисправностей
Особое место занимает таблица функций неисправности — наглядная и универсальная математическая модель ОД. Она особенно полезна для классификации основных принципов и процедур построения алгоритмов технического диагностирования РЭО и систем автоматики (СА).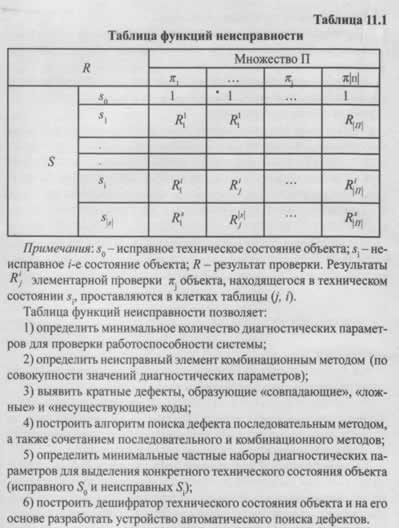
Классификация объектов диагностирования
При построении математических моделей объекты диагностирования РЭО и СА принято делить на две большие категории:Объекты непрерывного действия (непрерывные объекты), параметры которых рассматриваются как непрерывно изменяющиеся во времени. Примерами служат электрические цепи с резисторами, аналоговые системы автоматического регулирования, операционные усилители с обратными связями, электродвигатели.
Объекты дискретного действия (дискретные объекты), у которых значения параметров заданы на конечных множествах, а время отсчитывается дискретно. У таких объектов входные и выходные координаты зависят не только от технического состояния, но и от положения отдельных элементов. К ним относятся электрические цепи с контактными коммутаторами и системы логического управления.
Системы, содержащие в себе компоненты обоих типов, относятся к гибридным объектам. Классический пример гибридного объекта — аналого-цифровой преобразователь сигналов, сочетающий в себе непрерывные и дискретные процессы.

