В англоязычном сегменте интернета мне встретилась увлекательная статья, которая, как мне кажется, заслуживает внимания. Поскольку автоматический перевод часто искажает смысл, я подготовил адаптированный и выверенный перевод для всех интересующихся. Оригинал можно найти по ссылке. Надеюсь, чтение будет познавательным!
В конце XIX столетия математик Карл Вейерштрасс создал функцию, напоминающую фрактал. Коллеги поначалу восприняли её как нечто ужасное и противоестественное. Однако со временем это открытие кардинально изменило сами основы математической науки.
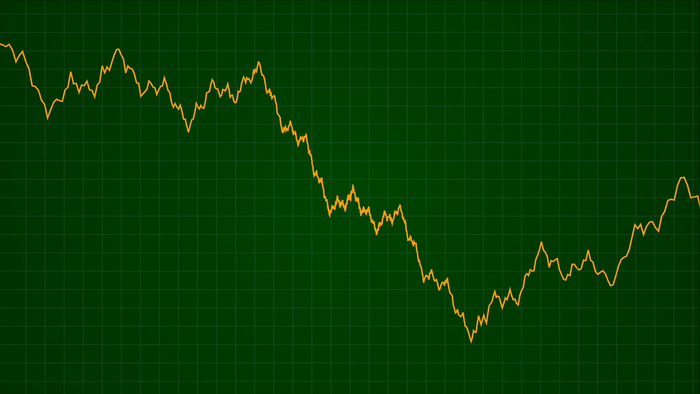
Если бесконечно увеличивать масштаб графика этой функции, её «зубчатая» и неровная структура будет проявляться всё сильнее, не сглаживаясь.
Кризис основ
Математический анализ, созданный в XVII веке, долгое время оставался мощным, но не до конца строгим инструментом. На протяжении веков его ключевые понятия часто опирались на интуитивные, а не на формально определённые концепции, что было нетипично для точных наук.
Как отмечает историк Майкл Барани, в XVIII–XIX веках вокруг исчисления сформировались две школы. Французские математики в целом были довольны его прикладными успехами в физике и астрономии. Немецкие же учёные, напротив, стремились к абсолютной строгости. Они искали контрпримеры, которые могли бы вскрыть слабости существующей теории и заложить более прочный фундамент.
Одним из лидеров этого движения стал Карл Вейерштрасс. Интересно, что его путь в математику был непрямым: отец настаивал на карьере в финансах, но Вейерштрасс, скучая на лекциях, увлекался фехтованием. Не имея степени, он стал школьным учителем, преподавая самые разные предметы — от математики до гимнастики.

Серьёзная математическая карьера Вейерштрасса началась лишь около 40 лет. Его одержимость логической строгостью в итоге привела к рождению современного анализа и появлению знаменитых «монстров».
Два столпа анализа: непрерывность и дифференцируемость
В 1872 году Вейерштрасс представил функцию, бросившую вызов всем привычным представлениям об исчислении. Работа была встречена частью коллег с непониманием и даже неприятием. Анри Пуанкаре назвал её «оскорблением здравого смысла», а Шарль Эрмит — «отвратительным злом».
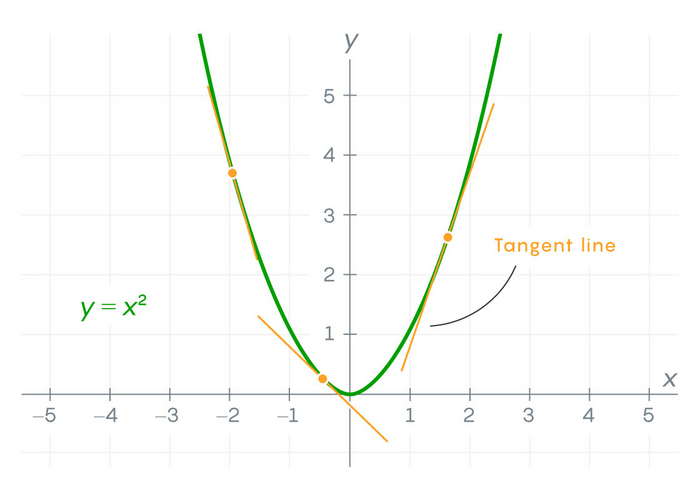
Чтобы понять причину такой реакции, нужно вспомнить основы. Непрерывная функция — это та, график которой можно нарисовать, не отрывая карандаша от бумаги. Анализ же изучает, как быстро меняются такие функции, используя понятие производной — скорости изменения, определяемой через касательную линию.
Если функция имеет разрыв, она не дифференцируема в этой точке. Но даже непрерывные функции могут иметь «углы», где производная не существует. Классический пример — функция модуля, график которой имеет вид буквы V.
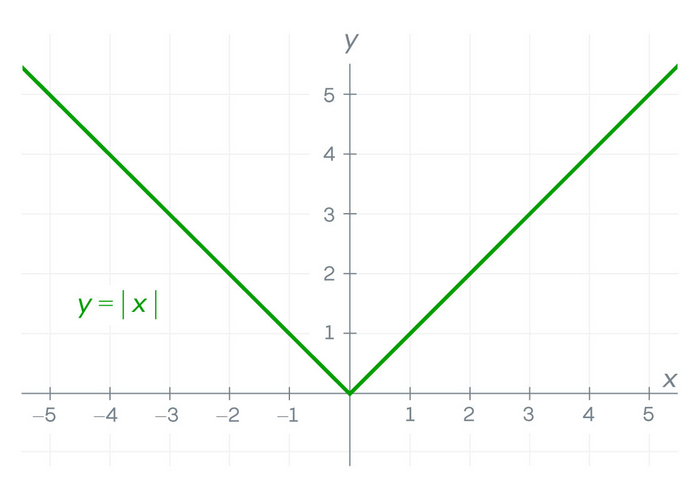
Слева от вершины наклон отрицательный, справа — положительный.
Обратите внимание: Нанороботы, вдохновленные человеком … будет создана сперма, которая исцелит наши тела.
В самой вершине направление резко меняется, и производная в этой точке не определена. Долгое время математики считали, что у непрерывной функции таких «проблемных» точек может быть лишь конечное число. Более того, в 1806 году Андре-Мари Ампер даже представил доказательство этого утверждения, которое долго не подвергалось сомнению.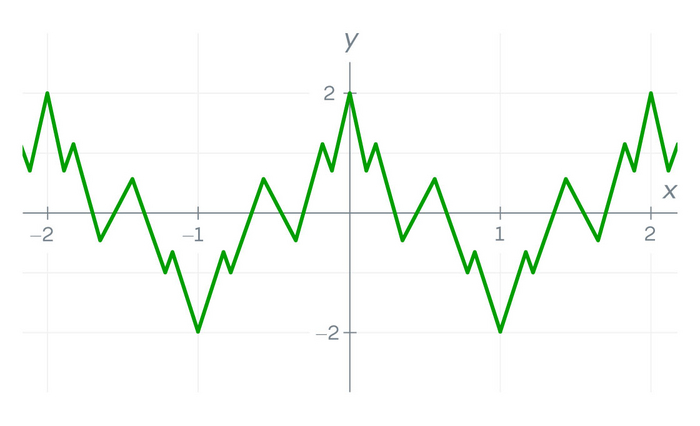
Рождение «чудовища»
Вейерштрасс опроверг это убеждение. Он построил функцию, которая была непрерывна в каждой точке, но при этом не имела производной ни в одной точке. Это было полным противоречием интуиции и «доказательству» Ампера.
Функция была построена как бесконечная сумма косинусов с быстро убывающими амплитудами и растущими частотами. Каждый новый член добавлял всё более мелкие «зубцы», и в пределе функция становилась бесконечно изрезанной, напоминая фрактал.
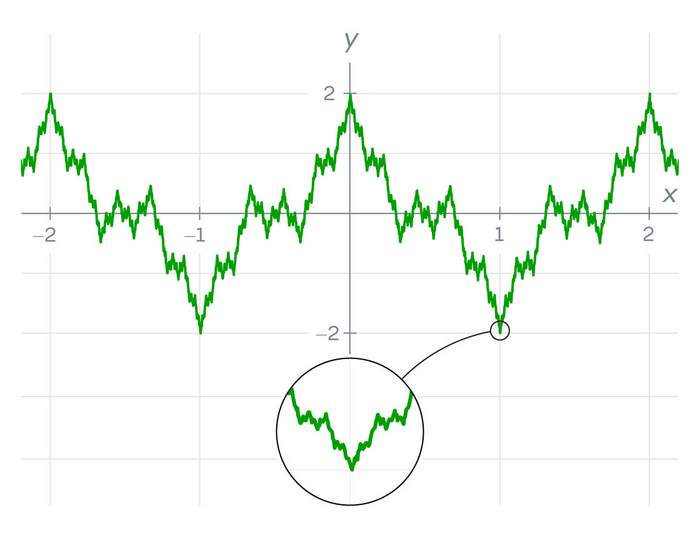
Многие современники отмахивались от этой конструкции как от патологической игрушки, не имеющей отношения к реальной математике. Действительно, при первом взгляде на график можно увидеть плавные участки. Но любое, сколь угодно сильное увеличение масштаба reveals всё новую и новую «шероховатость» — функция никогда не становится гладкой.
Ключом к строгому доказательству стал пересмотр самих определений. Вейерштрасс взял интуитивные формулировки Коши и Больцано и переписал их на безупречно точный язык эпсилон-дельта (этот подход теперь изучает каждый студент). Используя эти строгие определения, он показал, что его функция удовлетворяет критерию непрерывности, но для неё никогда не выполняется критерий дифференцируемости — предел, определяющий производную, расходится.
Наследие «монстра»
Это открытие имело далеко идущие последствия. Стало ясно, что математический анализ не может больше полагаться на геометрическую интуицию. Требовалась новая, абсолютно строгая основа. Работа Вейерштрасса заложила стандарты современного анализа и способствовала развитию теории функций.
Но значение «чудовища Вейерштрасса» вышло за рамки чистого анализа. Оно показало, что математика полна неожиданных, «диких» объектов, которые бросают вызов воображению. Как отмечает Филип Глейсман, эта функция открывает глаза на бесчисленное множество возможностей, скрытых во Вселенной.
Со временем нашлись и практические применения. В начале XX века подобные функции идеально подошли для моделирования броуновского движения — хаотического дрейфа частиц в жидкости. Они также используются в экономике для описания непредсказуемости финансовых рынков и в психологии для моделирования процессов принятия решений в условиях неопределённости.
История Вейерштрасса и его функции — это история о том, как то, что сначала кажется абсурдным и бесполезным, может со временем перевернуть науку и найти неожиданное применение. Подобные «монстры» продолжают вдохновлять математиков и учёных, напоминая о безграничной сложности и красоте математического мира.
Мой проект по науке и философии
[Моя] Наука Исследования Ученый Популярная наука Математика Видео Без звука Короткое видео Длинный текст 35Больше интересных статей здесь: Новости науки и техники.
Источник статьи: Рваная, чудовищная функция, которая сломала математический анализ.

