Автор: Денис Аветисян
Учёные совершили значительный шаг вперёд, разработав серию эффективных квантовых алгоритмов, предназначенных для моделирования сложнейших задач в гидродинамике. Эти алгоритмы способны работать с течениями жидкостей и решать нелинейные уравнения, которые долгое время оставались вычислительным вызовом для классических компьютеров.

В основе подхода лежит преобразование нелинейной динамики поля в линейную операцию с помощью метода Квантового Вейля-фон Неймана (KvN). Это преобразование реализуется на расширенном пространстве, а каждый шаг эволюции моделируется как локальное квантовое отображение, действующее на многомодовые когерентные состояния. В итоге весь алгоритм компилируется в логически эффективную, измеримую бинарную схему, глубина которой зависит от ранга Крауса, с последующей постселекцией определённого состояния.
Статья подробно анализирует применение методов троттеризации и тензорных сетей для моделирования динамики открытых квантовых систем, что особенно актуально для таких уравнений, как уравнения Навье-Стокса и Бюргерса.
Хотя теоретически квантовые компьютеры обладают огромным потенциалом для решения сложных дифференциальных уравнений, их практическая реализация на современном оборудовании сопряжена с серьёзными трудностями. В исследовании под названием «Provably Efficient Quantum Algorithms for Solving Nonlinear Differential Equations Using Multiple Bosonic Modes Coupled with Qubits» представлен инновационный аналоговый алгоритм. Он использует связанные бозонные моды и измерения кубитов, что позволяет обойтись без оцифровки гильбертова пространства. Этот подход с доказанной эффективностью моделирует эволюцию нелинейных уравнений в частных производных, требуя лишь O(T(log L + dr log K)) временных шагов, что подтверждено симуляциями уравнений Бюргерса и Фишера-КПП. Возникает ключевой вопрос: может ли эта схема стать фундаментом для создания практических квантовых алгоритмов, способных моделировать сложные физические системы на аналоговых квантовых устройствах ближайшего будущего?
Моделирование жидкостей: вызовы и пределы точности
Точное моделирование динамики жидкостей имеет критическое значение для множества приложений — от аэродинамики до климатологии. Однако традиционные численные методы часто сталкиваются с непреодолимыми трудностями при работе со сложными сценариями, такими как турбулентность, замысловатые граничные условия и многомасштабные явления. Существующие подходы могут быть либо чрезмерно затратными с вычислительной точки зрения, либо недостаточно точными для отображения тонких эффектов, особенно в переходных и высокотурбулентных режимах. Ключевая проблема заключается в поиске баланса между точным представлением физики и вычислительной реализуемостью. Каждая попытка создать идеальную симуляцию неизбежно упирается в будущий компромисс между этими двумя требованиями.
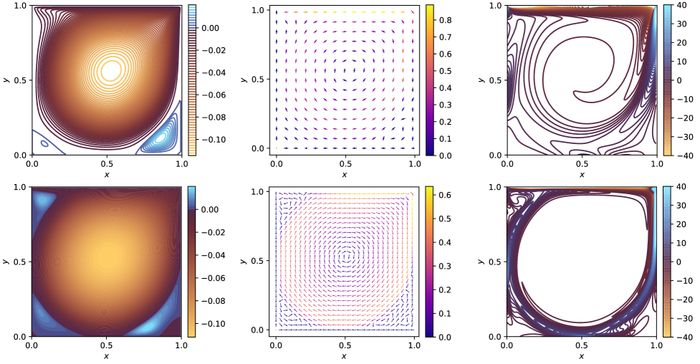
На примере моделирования течения в полости с движущейся крышкой на сетках 128×128 и 256×256 для разных чисел Рейнольдса (Re = 1000 и Re = 10000) показано, что результаты, полученные с помощью бозонного симулятора и метода Эйлера, отлично согласуются с данными прямого численного моделирования (DNS) для функций тока, полей скорости и завихренности.
Игнорирование этой фундаментальной задачи ведёт к созданию упрощённых моделей, которые дают неверные или вводящие в заблуждение результаты.
Синтез алгоритмов: троттеризация и TEBD
Алгоритм троттеризации предоставляет мощный инструмент для аппроксимации временной эволюции, необходимой для решения сложных уравнений, таких как уравнение Бюргерса или задача о вихревом течении. Его синергия с алгоритмом TEBD (Time-Evolving Block Decimation), основанным на тензорных сетях, приводит к радикальному снижению вычислительных затрат при сохранении высокой точности моделирования. В работе использовался согласованный временной шаг 10⁻⁵. Комбинация этих методов открывает двери для моделирования систем, которые ранее были недоступны для традиционных вычислительных подходов, благодаря оптимальному использованию ресурсов.

Симуляция уравнения Бюргерса с использованием тензорной сети и схемы TEBD на основе троттеризации демонстрирует, как начальный гауссов профиль скорости эволюционирует в ударную волну, которая затем сглаживается под действием вязкости. Профили скорости в различные моменты времени (t=0, 0.06, 0.12, 0.18) находятся в превосходном согласии с эталонным аналитическим решением.
Фазовое представление: моделирование открытых систем
Фазовое представление (Phase-Space Representation, PP) предлагает уникальный и мощный формализм для моделирования динамики открытых квантовых систем, используя функцию Глаубера-Сударшана для описания эволюции состояния. В рамках этого подхода амплитуды когерентных состояний используются для встраивания дискретных переменных в непрерывное фазовое пространство, что упрощает вычисления и повышает эффективность. Для реалистичного моделирования в PP-представление включены такие факторы, как потеря фотонов, а максимальное число фотонов ограничено значением 5 для контроля вычислительной сложности.
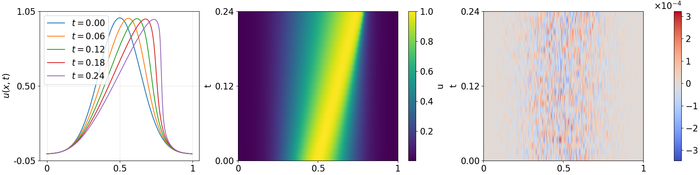
Валидация метода на примере одномерного уравнения Бюргерса показывает характерное смещение профиля скорости вправо, нелинейное усиление за счёт адвективного члена и диффузионное сглаживание благодаря вязкости. Карта u(x,t) демонстрирует преобладающий дрейф вправо со слабым вязким распространением. Систематическая ошибка, рассчитанная с использованием большого числа снимков, центрирована вокруг нуля и не имеет пространственной структуры, что подтверждает стабильность и точность метода.
Математический фундамент и техническая реализация
PP-представление опирается на строгий математический аппарат оператора плотности для описания квантового состояния. В практической реализации алгоритма используется метод конечных разностей для численного интегрирования, что обеспечивает эффективное вычисление PP-функции. Лемма Бейкера-Кэмпбелла-Хаусдорфа (BCH) играет решающую роль в выводе правил обновления состояния в процессе троттеризированной эволюции, гарантируя стабильность и точность всего алгоритма.
Будущие перспективы и новые горизонты
Комбинация методов троттеризации, TEBD и фазового представления открывает новые, ранее недостижимые возможности для моделирования сложной гидродинамики с беспрецедентной точностью.
Обратите внимание: СХПК «Новый путь» в Аликовском районе Чувашии открыл первую в республике роботизированную молочно-товарную ферму на 200 голов.
Исследование наглядно показывает, что сложные системы, описываемые уравнениями Навье-Стокса или Бюргерса, требуют не просто механического решения, а «взращивания» адаптивной модели, способной учитывать неизбежные погрешности. Подобно тому, как квантовые алгоритмы используют суперпозицию состояний, эта работа стремится охватить неопределённость, присущую динамике жидкостей. Как отмечал Вернер Гейзенберг: «Чем больше мы узнаем, тем больше понимаем, чего не знаем». Эта мысль находит прямое отражение в представленном исследовании, где точность вычислений ограничена необходимостью аппроксимаций, и каждый шаг вперёд открывает новые нерешённые вопросы. Применение методов Троттера и тензорных сетей — это не столько построение идеальной модели, сколько создание «экосистемы», способной к самокоррекции и эволюции перед лицом вычислительного хаоса.
Что ждёт впереди? Взгляд за горизонт
Представленные методы, несмотря на свою впечатляющую эффективность, по сути лишь отодвигают неизбежное. Разделение системы на более мелкие, управляемые части — будь то с помощью троттеризации или тензорных сетей — не отменяет её фундаментальной сложности и хрупкости. Каждое увеличение детализации модели — это одновременно и пророчество о потенциальном будущем коллапсе вычислений, о синхронном отказе всех взаимосвязанных компонентов. Увеличение числа бозонных мод и кубитов лишь усложняет общую картину, не решая коренную проблему взаимозависимости.
Более того, переход к PP-представлению для динамики открытых систем — это не окончательное решение, а скорее смещение фокуса с одной проблемы на другую. Управление сложностью не равнозначно её устранению. Вместо бесконечной погони за «доказуемо эффективными» алгоритмами, возможно, следует признать, что любая система, стремящаяся к абсолютной точности, неизбежно приближается к критической точке, где даже малый внешний шум может вызвать каскадный отказ.
Следующий этап, вероятно, будет посвящён не поиску ещё более совершенных инструментов моделирования, а изучению принципов самовосстановления и устойчивости в сложных системах. Ключевой вопрос заключается не в том, как построить идеальную модель, а в том, как смириться с её неизбежной неидеальностью и научиться предсказывать — а возможно, и смягчать — последствия её распада. В конечном счёте, всё стремится к взаимозависимости, и это — не ошибка, а фундаментальный закон сложных систем.
Оригинал статьи: https://arxiv.org/pdf/2511.09939.pdf
Связаться с автором: linkedin.com/in/avetisyan
Больше интересных статей здесь: Производство.
Источник статьи: Квантовые симуляции: новый подход к решению уравнений гидродинамики.

