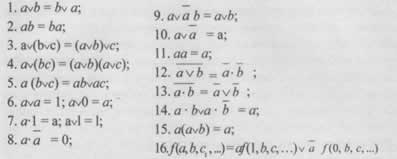Суть логико-вероятностных методов расчета надежности состоит в описании схемы системы с помощью аппарата математической логики с последующим использованием теории вероятностей при определении характеристик надежности.
Произвести расчет надежности системы - значит определить связь между сложным событием-отказом системы и простыми событиями. Следовательно, в основу расчетов систем на надежность положены операции с событиями и высказываниями. Такие операции рассматриваются в разделе математической логики - алгебре высказываний. Объектом ее исследований являются высказывания, о которых можно утверждать, что они либо истинны, либо ложны. Высказывания могут быть простыми и сложными. Сложное высказывание состоит из простых высказываний, соединенных между собой логическими операциями. Каждая из логических операций устанавливает вполне определенную связь между истинностью сложного и простых высказываний.
Наиболее распространенные логические операции для двух простых высказываний а и Ъ приведены в табл. 7.1. Истинность высказываний обозначена «1», ложность - «0»(1 - элемент работоспособен, 0 -элемент неработоспособен).
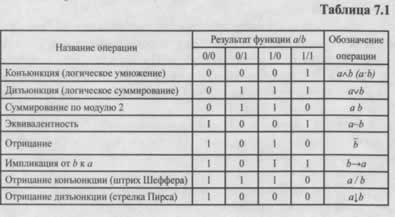
Переход от любого сложного высказывания к высказыванию, содержащему операции конъюнкции, дизъюнкции и отрицания, необходимо осуществлять в такой последовательности:
1) из таблицы выделить наборы простых высказываний, приводящие сложное высказывание в единицу;
2) для каждого из таких наборов записать простые истинные высказывания без знака отрицания, а ложные - со знаком отрицания; полученные высказывания соединить знаком конъюнкции;
3) конъюнкции простых высказываний соединить операцией дизъюнкции.
При расчетах надежности наиболее часто используются законы и правила преобразований сложных высказываний. С помощью этих правил сложную логическую функцию можно привести к минимальной бесповторной форме, т. е. к виду, когда функция содержит минимальное число составляющих и в ней нет повторения одинаковых аргументов: