Параллельно-последовательная структура надежности системы дает представление о связи между надежностью системы и ее элементами. Расчет надежности ведется последовательно от элементарных узлов структуры к ее все более сложным узлам и сводится к расчету отдельных участков схемы, состоящих из параллельно и последовательно соединенных элементов.
Например, на рис. 7.16 узел, состоящий из элементов 1 - 2, является элементарным, а узел, состоящий из элементов 1 - 2 - 3 - 4 - сложным. Эта структура может быть сведена к эквивалентной, состоящей из узла (1-2-3 -4) и элемента 5, соединенных последовательно.
Расчетные формулы для элементов, соединенных параллельно.
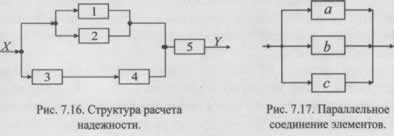
Рассмотрим параллельное соединение, состоящее из трех элементов (рис. 7.17). Отказ такого соединения произойдет после выхода из строя всех элементов. Соединение будет работоспособным, если работоспособны элемент а, или элемент b, или элемент с, или элементы awb, а и с, b и с, а и b и с. Этим условиям соответствует функция алгебры логики (ФАЛ), где а, b, с - события, состоящие в том, что элементы а, Ь, с находятся в работоспособном состоянии:
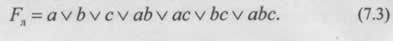
ФАЛ, связывающую состояние элемента с состоянием системы, называют функцией работоспособности системы 
. Для оценки работоспособных состояний системы вводят два понятия: 1) кратчайший путь успешного функционирования, представляющий собой такую конъюнкцию элементов, ни один из компонентов которой нельзя изъять, не нарушив условия функционирования системы; 2) минимальное сечение отказов - конъюнкция из отрицаний элементов, ни один из компонентов которой нельзя изъять, не нарушив условия неработоспособности системы. Используя эти понятия, условия работоспособности системы можно записать либо в виде дизъюнкции всех кратчайших путей успешного функционирования - дизъюнктивная нормальная форма (ДНФ), либо в виде конъюнкции отрицаний всех минимальных сечений отказов - конъюнктивная нормальная форма (КНФ).
После составления функции работоспособности системы в виде ДНФ или КНФ необходимо перейти к вероятностной функции, с помощью которой определяются характеристики надежности. Однако непосредственно перейти к вероятностной функции от ДНФ или КНФ нельзя, так как одна и та же переменная может входить в состав нескольких конъюнкций (7.3). Поэтому полученное выражение (7.3) необходимо преобразовать к бесповторной форме функции алгебры логики (БФАЛ). Имеется несколько алгоритмов преобразования ФАЛ в БФАЛ: алгоритмы С.В. Макарова, Ю.Б. Мерекина, И.А. Рябинина, А.С. Смирнова и др.
Минимизируем выражение (7.3):
