В инженерной практике для оценки надежности систем широко применяются расчеты, основанные на анализе параллельно-последовательных структур. Их популярность объясняется относительной простотой преобразований. Однако не все системы, особенно сложные, могут быть представлены в виде такой структуры. Для анализа надежности подобных систем существуют альтернативные подходы. К ним относятся:
а) преобразование схемы с помощью эквивалентной замены треугольника на звезду (или обратной замены);
б) метод разложения сложной структуры по базовому (ключевому) элементу.
Алгоритм логико-вероятностного метода
Логико-вероятностный метод представляет собой системный подход к расчету надежности и включает в себя последовательность четких шагов:
- Формулировка условия работоспособности системы на естественном языке.
- Перевод словесного условия в формальную логическую функцию, которая описывает все состояния системы, приводящие к ее работоспособности.
- Минимизация полученной логической функции и приведение ее к так называемой бесповторной форме, где каждый элемент встречается только один раз. Это упрощает дальнейшие вычисления.
- Арифметизация функции — замена логических операций (И, ИЛИ, НЕ) на арифметические (умножение, сложение, вычитание).
- Непосредственный расчет вероятности: замена логических переменных (событий) на числовые значения их вероятностей безотказной работы.
- Вычисление итоговой вероятности безотказной работы системы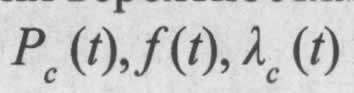 
и других важных показателей надежности.
- Критический анализ и интерпретация полученных результатов для принятия инженерных решений.
Практический пример расчета
Пример 1. Рассмотрим систему, структурная схема надежности которой представлена на рисунке 7.18. Требуется определить вероятность безотказной работы всей системы, если известны вероятности безотказной работы каждого ее элемента (значения указаны на схеме).
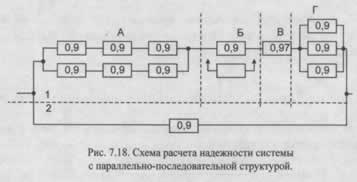
Решение. Анализ схемы (рис. 7.18) показывает, что система состоит из двух устройств с разной надежностью (устройство 1 и устройство 2). Устройство 1 имеет сложную структуру и включает четыре узла:
Узел А: использует постоянное (нагруженное) дублирование (резервирование с кратностью m=1). Каждая из двух параллельных цепей состоит из трех элементов, соединенных последовательно с точки зрения надежности.
Узел Б: зарезервирован по способу замещения (ненагруженный резерв) с кратностью m=1.
Узел В: нерезервированный, содержит всего один элемент.
Узел Г: применяется резервирование с дробной кратностью (схема "m из l"), где общее число элементов l=3, а для работоспособности требуется не менее m=2.
Устройство 2 является нерезервированным, и его надежность задана. Поскольку устройства соединены последовательно в смысле надежности, вероятность безотказной работы всей системы равна произведению вероятностей работы каждого устройства:
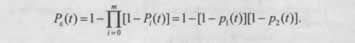
Найдем вероятность P1(t) для устройства 1. Она определяется как произведение вероятностей безотказной работы всех его узлов (A, Б, В, Г), так как узлы соединены последовательно:
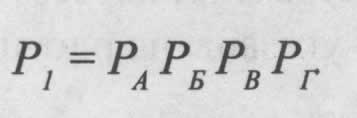
Рассчитаем надежность каждого узла:
1. Для узла А (общее резервирование, m=1, n=3 в каждой цепи):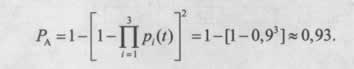
2. Для узла Б (резервирование замещением, m=1):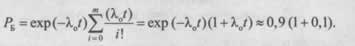
Для вычисления интеграла 
удобно использовать разложение в ряд Тейлора:
3. Для узла Г (резервирование с дробной кратностью, схема "2 из 3"): вероятность того, что из трех элементов работоспособны не менее двух. Расчет ведется по формуле:
Подставив все вычисленные значения в формулу для P1(t), а затем и в формулу для Pс(t), получим итоговую вероятность безотказной работы всей системы. Численные значения подставляются в соответствии с данными на исходной схеме.