В основе аналитического прогнозирования лежит разделение временного поведения объекта на два ключевых интервала. Первый интервал (T1) — это период наблюдения, когда собираются данные о поведении объекта. Второй интервал (T2) — это будущий период, для которого и строится прогноз. Логично предположить, что чем длиннее интервал наблюдения T1, тем больше информации о процессе мы получаем, а значит, прогноз становится более достоверным. Однако на практике удлинение T1 связано с ростом затрат — как на проведение длительных экспериментов, так и на обработку больших массивов данных. Поэтому специалисты стремятся найти оптимальный баланс, сокращая T1 до минимально необходимого уровня без существенной потери точности прогноза.
Экстраполяция как основа прогнозирования
Суть прогнозирования изменения состояния объекта заключается в применении методов экстраполяции. Это означает, что выявленные в прошлом (на интервале T1) тенденции развития объекта переносятся на будущее (интервал T2). Прогноз строится на основе детерминированных характеристик объекта, полученных в ходе наблюдений или специально спланированных экспериментов.
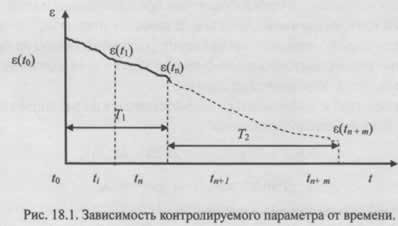
Ключевое допущение метода экстраполяции состоит в том, что условия работы объекта, наблюдавшиеся в прошлом, останутся неизменными в будущем или будут изменяться по заранее известному закону. Именно это предположение позволяет экстраполировать тренды.
Источники погрешностей и суть аналитического прогнозирования
Точность прогноза, построенного методом экстраполяции, зависит от нескольких факторов. Во-первых, это погрешности измерения и фиксации данных в ходе наблюдений. Во-вторых, ошибки, возникающие при построении самой математической модели (прогнозирующего выражения). И в-третьих, что особенно важно, — погрешность, связанная с неопределенностью условий в будущей области T2, которая может отличаться от условий в T1.
Совокупность методов экстраполяции, используемых для вычисления значений прогнозируемых переменных, и образует область аналитического прогнозирования.
Критерии выбора прогнозируемых параметров
Перед построением математической модели необходимо правильно выбрать параметры, которые будут прогнозироваться. Эти параметры должны обладать важным свойством — чувствительностью к управляющим воздействиям (факторам). Любое изменение фактора должно находить отражение в динамике выбранного параметра. В случае многофакторного анализа также требуется обеспечить совместимость и сопоставимость всех используемых параметров.
Например, при прогнозировании состояния электронного усилителя в качестве прогнозируемого параметра может выступать его коэффициент усиления (Kу). А в роли наблюдаемых факторов (влияющих на Kу) — температура окружающей среды и время эксплуатации усилителя.
Математические модели в прогнозировании
Для прогнозирования технического состояния объектов часто применяются различные математические модели. Одной из наиболее распространенных является экспоненциальная модель вида W(t) = a * exp(b*t), где a и b — коэффициенты, которые рассчитываются на основе экспериментальных данных e(ti).
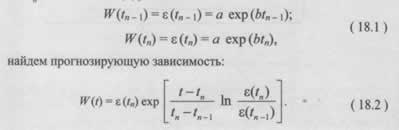

Коэффициенты a и b определяются путем решения системы уравнений, составленной для двух контрольных точек, например, e(tn-1) и e(tn). Экспоненциальная модель хорошо подходит для описания процессов, характер изменения которых близок к экспоненциальному (например, процессы износа, старения, накопления отказов). Однако стоит отметить, что кривая, построенная всего по двум точкам, часто оказывается слишком грубым приближением и может неточно отражать реальную динамику сложных процессов.
Экспоненциальная зависимость также может описывать связь между двумя параметрами, например, y(x). Если же прогнозируемый параметр зависит от двух или более факторов одновременно, для построения модели обычно переходят к более сложным полиномиальным зависимостям, которые позволяют учесть многомерное влияние.

