Задача поиска дефекта может быть решена аппаратными или программными средствами.
При решении данной задачи, так же, как и при функциональном диагностировании, используются комбинационный и последовательный методы тестирования. В первом случае анализируется лишь комбинация исходов всех элементарных тестов, порядок исполнения которых может быть произвольным, во втором случае - исход каждого очередного теста.
Последовательное тестирование может быть упорядоченным, когда отдельные элементарные тесты используются в некоторой заранее фиксированной последовательности, и условным, когда выбор каждого следующего теста зависит от результата предыдущего.
Комбинационный метод применяется в основном при вводе устройства в эксплуатацию или возникновении аварийных ситуаций, когда возможен выход из строя нескольких элементов. Последовательный метод чаще используется при внезапном отказе объекта во время его использования по назначению, когда высока вероятность отказа одного элемента системы.
Критерием оптимальности системы диагностирования, реализуемой программными средствами, является либо время, затрачиваемое на тестирование, либо необходимый объем памяти, либо трудоемкость проведения теста, либо некоторый (комбинированный) экономический критерий.
Метод построения квазиоптимальных тестов Шеннона-Фано
Допустим, что в диагностируемом объекте имеется одна неисправность (типа постоянный «О» или постоянная «1»), Каждой из неисправностей присваивается вероятность р. того, что имеет место именно данная i-я неисправность. Согласно сделанному допущению = 1. Вероятность можно определить с помощью одного из известных методов расчета надежности.
Первый тест выбирается так, чтобы он разделил множество возможных неисправностей объекта на два подмножества с примерно равными суммарными вероятностями входящих в них неисправностей. Тест должен определить, в какое подмножество входит имеющаяся неисправность. Затем выбирается тест, разделяющий это подмножество на приблизительно равновероятные подмножества. После этого определяют подмножество, в котором, как было установлено, находится неисправность, и т. д. до достижения полной или достаточной определенности относительно местонахождения неисправности.
Пусть исходной для построения алгоритма методом Шеннона - Фано является таблица покрытий контрольных тестов.
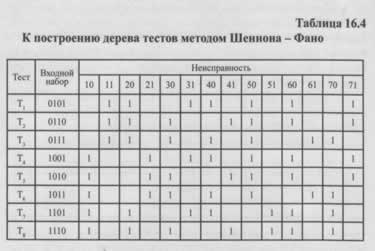
Допустим, что все 14 неисправностей равновероятны. В качестве первого теста выбирается тест Т1, разделяющий в зависимости от исхода теста (обнаруживается неисправность или нет) все возможные неисправности на два подмножества: {10,21,30,41, 51,61,70} и {11, 20,31,40, 50, 60,71}.
Предположим, что тест Т1 не обнаружил неисправность, тогда неисправность входит в первое подмножество. В качестве следующего теста может быть выбран тест Т3, разделяющий первое подмножество на подмножества: {10,21, 41, 51} и {30, 61, 70}.
Таким образом, строится полное диагностическое дерево (рис. 16.6), позволяющее за 3-4 теста определить, какая из 14 неисправностей имеет место в данной схеме. Метод Шеннона - Фано можно отнести к зондовой организации тестирования, так как каждый последующий тест выбирается исходя от результатов предыдущего теста.
В случае диагностирования сложных схем применяют разделение диагностируемой логической схемы на более простые составляющие, т. е. декомпозицию объекта. Декомпозицию целесообразно проводить так, чтобы в результате схема была представлена в виде совокупности подсистем с одним выходом,

т. е. декомпозицию объекта. Декомпозицию целесообразно проводить так, чтобы в результате схема была представлена в виде совокупности подсистем с одним выходом.

