Хотя квадрат, треугольник, ромб, круг и трапеция кажутся основой нашего геометрического мира, природа продолжает преподносить сюрпризы. Совсем недавно учёные обнаружили целый новый класс геометрических форм, способных идеально заполнять пространство без зазоров и наложений. Эти формы, получившие название «мягкие клетки», встречаются в самых неожиданных местах: в структуре мышечных клеток и в сложных изогнутых раковинах моллюсков, таких как наутилус.
Наука о покрытии пространства
Математическая дисциплина, известная как теория замощения или тесселяции, уже давно изучает способы заполнения плоскости или объёма фигурами без промежутков. Традиционно для этого использовались формы с чёткими углами — треугольники, шестиугольники или правильные многогранники. Однако наблюдения за природой показывают, что она часто обходится без острых углов, предпочитая более плавные и изогнутые контуры. «Похоже, природа не только не терпит пустоты, но и испытывает неприязнь к острым углам», — отмечает Ален Гориэли, профессор математического моделирования из Оксфордского университета, соавтор исследования. Примеры таких «мягких» природных мозаик можно найти в концентрических слоях луковицы или в круговом расположении мышечных клеток, что ставит перед математиками сложную задачу по объяснению этих естественных структур.
Вдохновение от мозаики Пенроуза
Вдохновившись знаменитой непериодической мозаикой Пенроуза, открытой в 1980-х годах, международная группа математиков под руководством Габора Домокоша из Будапештского университета технологии и экономики совместно с коллегами из Оксфорда взялась за решение этой задачи. В своём исследовании, опубликованном в журнале Труды Национальной академии наук, они заново изучили принципы периодического замощения и в итоге открыли новый класс фигур — мягкие клетки.
Обратите внимание: Треугольные, квадратные и пятиугольные числа, и где они встречаются в жизни.
Как поясняют авторы работы, эти формы минимизируют количество острых углов и при этом способны полностью покрывать пространство, не перекрываясь.
На иллюстрации показана мягкая версия усечённого октаэдра — классического архимедова тела, преобразованного в «мягкую клетку».Два измерения против трёх: парадокс углов
В ходе исследования команда провела эксперименты с использованием специально разработанной алгоритмической модели. Они обнаружили любопытный парадокс: в двумерном пространстве мягкие клетки проявляются как фигуры всего с двумя углами. Подобные узоры можно увидеть в некоторых архитектурных решениях, а также в биологических тканях. Однако в трёх измерениях эти структуры демонстрируют гораздо большую сложность и гладкость. «Мягкие клетки помогают понять, почему на поперечном срезе раковины мы видим углы камер, но не можем разглядеть их истинную трёхмерную геометрию», — объясняет Габор Домокош.
Изучая камеры наутилуса, учёные заметили, что на срезах действительно видны острые углы. Но когда они проанализировали внутреннюю трёхмерную структуру с помощью компьютерной томографии, то обнаружили совершенно иную картину — плавные, изогнутые поверхности без резких граней. Домокош отметил, что дальнейший анализ раковин принёс неожиданные результаты: их поперечные сечения соответствуют двумерным мягким клеткам с двумя углами, но в объёме эти углы исчезают.
«Хотя в плоскости мы наблюдаем два угла, создаётся впечатление, что в трёхмерном пространстве углов нет вообще», — подтверждает соавтор исследования Кристина Регос. Детальные томограммы показали, что камеры наутилуса представляют собой идеальные примеры трёхмерных мягких клеток, которые заполняют объём раковины под любым углом, образуя бесшовную структуру.
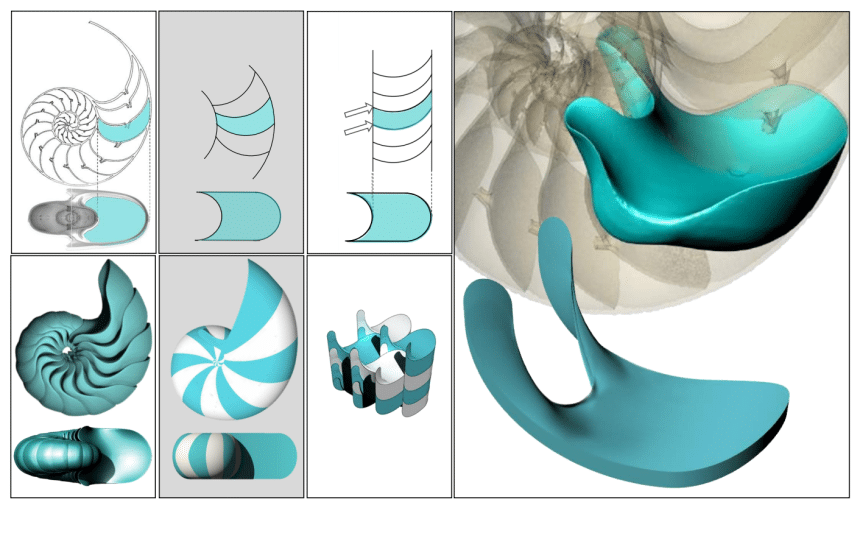На изображении слева показано поперечное сечение камеры раковины с видимыми углами. Справа — трёхмерная модель той же камеры, где углы полностью сглажены, демонстрируя свойства мягкой клетки.Новые горизонты для математики и биологии
«Мир многоугольников и многогранных замощений настолько богат и интересен, что математикам даже не нужно искать новые игровые площадки — они сами расширяются», — с энтузиазмом добавляет Домокош. Исследователи приходят к выводу, что отсутствие острых углов и наличие гладкой, сильно изогнутой геометрии делают мягкие клетки идеальной математической моделью для описания биологических структур, которые формируются и растут в условиях пространственных ограничений, будь то раковина моллюска или ткань живого организма.
Больше интересных статей здесь: Новости науки и техники.
Источник статьи: Квадрат, треугольник, ромб, круг и трапеция — одни из самых знакомых геометрических фигур.