В сложных радиоэлектронных системах и средствах автоматики на стадии эксплуатации действуют две совокупности процессов: первая совокупность - деградационные процессы, ухудшающие состояние системы с точки зрения безотказности и выводящие параметры за пределы допуска.
Вторая совокупность - стабилизирующие процессы, обеспечивающие сопротивление развитию деградации, поддерживающие работоспособность системы или восстанавливающие, парирующие ухудшение её технического состояния.
Ко второй совокупности процессов относятся такие, как настройка и регулировка параметров при функциональном использовании (автоматическая регулировка усиления - АРУ, автоподстройка частоты - АПЧ и др.), а также подстройки и регулировки, возникающие в результате замены элементов на этапах технического обслуживания и ремонта.
Процесс настройки любого объекта на оптимальный режим его работы в ряде случаев представляет определённую сложность и требует знания методов настройки, особенно когда настройке подлежат два и более параметров.
Рассмотрим некоторые из них. Предположим, что показатель качества работы системы J нам известен и измеряется количественно. Зависимость этого показателя от параметра настройки имеет экстремум (максимум или минимум), однако положение этого экстремума априори неизвестно. Требуется найти такие соотношения варьируемых параметров хi, при которых показатель качества J принимал экстремальное (наилучшее) значение.
Рассмотрим самый простой случай, когда количество настраиваемых параметров k = 1.
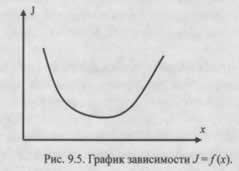
На рисунке 9.5 обозначены: x- параметр настройки, J- показатель качества.
Параметром настройки может служить сопротивление резистора, ёмкость конденсатора, а также положение рукоятки переменного резистора или переменного конденсатора и др., выраженные в единицах измерения (Ом, мкФ) или в угловых градусах, делениях шкалы изменения сопротивления, емкости и т. п.
Проведя эксперимент в одной точке и выбрав шаг изменения параметра, можно легко определить направление движения к оптимуму и совершить это движение. Для этого потребуется провести дополнительно эксперимент еще в одной точке х.
Ситуация усложняется при наличии двух варьируемых параметров.
В этом случае рекомендуется использовать методы, основанные на теории планирования эксперимента.
Теория планирования эксперимента дала в руки специалиста по настройке несколько методов поиска оптимальных соотношений параметров системы, как в статическом, так и в динамическом режимах. К ним относятся метод крутого восхождения (метод движения по градиенту), метод эволюционного планирования Бокса, метод последовательного симплексного планирования и его различные модификации. Из всех перечисленных методов наиболее приемлемым для оптимизации РЭО и СА является метод последовательного симплексного планирования или последовательный симплекс-метод (ПСМ) как наиболее простой и устойчивый к внутренним и внешним помехам. Последнее особенно ценно для настройки судовых объектов.
Принцип симплексного планирования состоит в том, что условия первой серии опытов в многомерном пространстве соответствуют координатам точек, образующих симплекс. Симплекс образованный k + 1 точками, расположенными на равном расстоянии друг от друга в k-мерном пространстве, называется правильным. В одномерном пространстве симплекс представляет собой отрезок прямой, при двух факторах - равносторонний треугольник, при трех - тетраэдр. Для симплекса большей размерности геометрического представления не существует, но это не мешает настраивать системы с большим числом параметров настройки. При поиске оптимума симплекс определенным образом перемещается (кантуется) по поверхности отклика.
Перемещение симплекса по поверхности отклика выполняется в следующей последовательности. Из опытов первой серии в вершинах правильного симплекса выбирается точка с наихудшим результатом. Затем определяются координаты новой точки, представляющей собой зеркальное отражение точки с наихудшим результатом относительно противоположной грани симплекса, причем грань в этом случае образуют точки k-мерного симплекса. Если этой новой точкой заменить точку с наихудшим результатом, то образуется новый правильный симплекс, смещенный в общем случае в сторону улучшения результата. В этой новой точке ставится опыт, результат которого сопоставляется с результатами в оставшихся точках. Выбирается опыт, в котором был получен наихудший результат, и находится его зеркальное отображение и т. д. Таким образом, осуществляется перемещение (кантование) симплекса до тех пор, пока не будет достигнута область оптимума. Пояснить процесс кантования симплекса можно на примере с двумя факторами, симплекс при этом представляет собой правильный треугольник.
На рисунке 9.6 изображен порядок постановки опытов при симплексном планировании. В первой серии ставятся k+1 опытов (точки 1, 2, 3). Последующее кантование симплекса осуществляется путем анализа полученных результатов и сравнения их с результатами опытов в других точках, при этом на каждом шаге реализуется только один опыт. Наихудший результат был получен в точке 1 как наиболее удалённой от оптимума.
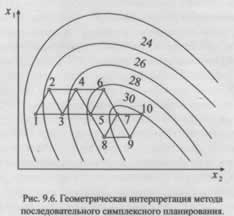
Симплекс поворачивается вокруг грани 2 - 3 и в точке 4 ставится опыт. Теперь анализируются результаты опытов в точках 2,3 и 4. Затем поворот симплекса осуществляется вокруг грани 3-4. Определяются координаты точки 5, в которой снова ставится один опыт. Дальнейшее движение симплекса по поверхности отклика понятно из рис. 9.6.
С выбора исходного симплекса начинается процедура оптимального выбора параметров. Ниже приводятся координаты исходного симплекса для трёх и более параметров оптимизации. Заметим, что координаты исходного симплекса для трёх параметров заданы целочисленной матрицей. Это же условие выполняется при настройке системы с семью варьируемыми параметрами (k = 7).
Очевидно, что чем больше размеры исходного симплекса, тем быстрее его продвижение к области оптимума. По мере продвижения к области оптимальной настройки размеры симплекса можно уменьшать. При выборе размеров симплекса возможен учет дискретного характера параметров настройки.
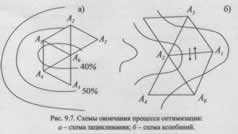
На рис. 9.7 представлены два случая, сигнализирующие о конце оптимизации при настройке объекта по двум параметрам.
Признаками конца настройки системы являются процесс зацикливания симплекса - поворот симплекса вокруг одной вершины (рис. 9.7, а), либо процесс колебания вершины симплекса относительно одной грани (рис. 9.7, б).
Координаты вершины нового симплекса в общем случае рассчитываются по формуле:
где N = k+ 1 - число точек в исходном симплексе; Xj, N+1- координата новой точки в натуральных величинах для фактора с номером j; X*j - координата данного фактора в отвергнутом опыте.


