Расчеты надежности, основанные на использовании параллельно-последовательных структур, получили наибольшее распространение в инженерной практике благодаря относительной простоте преобразований. Однако условие работоспособности не всегда можно представить параллельно-последовательной структурой. В таких случаях можно:
а) осуществить преобразование с эквивалентной заменой треугольника на звезду и обратно;
б) разложить сложную структуру по базовому элементу.
Расчет надежности систем логико-вероятностным методом предполагает выполнение следующих операций:
- словесная формулировка условий работоспособности системы;
- составление логической функции работоспособности;
- минимизация функций и приведение ее к бесповторной форме;
- арифметизация функции;
- замена событий (высказываний) их вероятностями;
- расчет надежности (определение 
) и других характеристик);
- анализ полученных результатов.
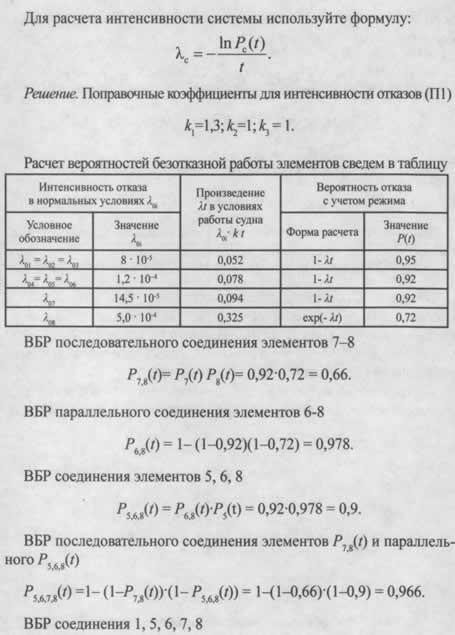
Пример 1. Дана система, схема расчета надежности которой изображена на рис. 7.18. Необходимо найти вероятность безотказной работы системы при известных вероятностях безотказной работы ее элементов (значения вероятностей указаны на рисунке).
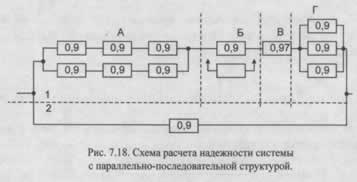
Решение. Из рис. 7.18 видно, что система включает в себя два неравнонадежных устройства 1 и 2. Устройство 1 состоит из четырех узлов:
А - дублированный, с постоянно включенным резервом; в каждой части узла имеется три последовательно соединенных (в смысле надежности) элемента расчета;
Б - дублированный по способу замещения;
В - с одним нерезервированным элементом;
Г - резервированный, с кратностью т = 1/2 (схема группирования).
Устройство 2 нерезервированное, его надежность известна. Так как оба устройства неравнонадежны, то вероятность безотказной работы всей системы равна:
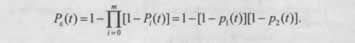
Найдем вероятность Pt(t). Вероятность безотказной работы устройства 1 равна произведению вероятностей безотказной работы всех узлов:
В узле А используется общее резервирование с кратностью m = 1. При этом число элементов основной и резервной цепей n = 3. Следовательно:
В узле Б кратность резервирования замещением m = 1, тогда вероятность безотказной работы этого узла:
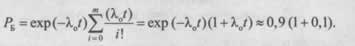
Для вычисления
используем разложение в ряд Тейлора:
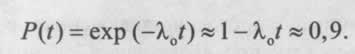
В узле Г применено резервирование с дробной кратностью, когда общее число основных и резервных систем 1 = 3, число систем, необ
