Расчет наработки на отказ для отдельных устройств
Рассмотрим практические ситуации, когда необходимо оценить надежность оборудования, способного к восстановлению после сбоев. В первом примере анализируется работа судовой радиолокационной станции (РЛС). За определенный период наблюдения было зафиксировано 10 отказов. Начальные показания счетчика наработки составляли 272 часа, а конечные — 3 272 часа. Для определения среднего времени работы между отказами (наработки на отказ) необходимо сначала вычислить общую наработку за наблюдаемый интервал.
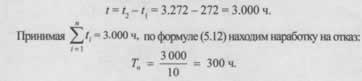
Во втором примере задача усложняется: оценивается надежность эхолотов одной модели, установленных на трех разных судах. Статистика отказов и наработки для каждого прибора различается: первый эхолот отказал 7 раз при наработке 6 250 часов, второй — 10 раз при 5 300 часах, третий — 8 раз при 7 200 часах. Чтобы получить обобщенный показатель надежности для данной марки, сначала находится суммарная наработка всех трех устройств, а затем общее количество отказов.

Оценка вероятности безотказной работы для группы устройств
Третий пример демонстрирует подход к оценке надежности для большого парка однотипного оборудования. В течение 1 800 часов наблюдалась работа 600 РЛС. За этот период отказали 30 устройств. Ключевым показателем здесь является вероятность безотказной работы, которая показывает, какая доля оборудования успешно проработает заданное время.
Решение начинается с определения количества исправных РЛС к концу периода наблюдения:
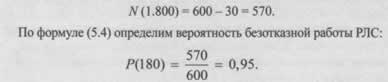
Полученное значение вероятности интерпретируется следующим образом: в среднем 95 из каждых 100 РЛС данной модели будут работать без сбоев в течение 1 800 часов. Это важный статистический показатель для планирования технического обслуживания и создания резервного фонда оборудования.

Анализ надежности сложной восстанавливаемой системы
Шестой пример рассматривает более сложную систему — двухканальную линию передачи информации, работающую непрерывно. Особенность системы в том, что для восстановления любого отказавшего канала необходимо останавливать всю линию, что приводит к потере информации. Интенсивность потерь зависит от количества неработающих каналов. Известны интенсивность отказов (λ) и интенсивность восстановления (μ) для каждого канала, причем время работы и время восстановления подчиняются экспоненциальному распределению.
Ставится оптимизационная задача: определить, при каком количестве отказавших каналов следует останавливать линию для восстановления, чтобы минимизировать средние потери информации. Рассматриваются две стратегии восстановления при отказе обоих каналов: последовательное (поочередное) и параллельное (одновременное) восстановление.
Решение задачи строится на составлении графов состояний системы. В простейшем случае, когда восстановление начинается при отказе одного канала (r=1), система может находиться только в двух состояниях: оба канала работают, или оба канала остановлены на восстановление. Анализ переходов между этими состояниями позволяет найти стационарные вероятности и рассчитать средние потери.


