Для обработки результатов двухфакторных экспериментов, расчета коэффициентов и построения графиков были созданы два программных продукта. Программы написаны в среде Borland Delphi 5.0 и предназначены для работы в ОС Windows 9х и Windows ХР. Во всех программах предусмотрено сохранение результатов и вывод их на печать.
Программные продукты предназначены для работы с результатами двухфакторного эксперимента и ориентированы на совместное использование (что, впрочем, не исключает и раздельный вариант работы).
Программа ориентирована на расчет коэффициентов двухфакторной модели по результатам активного эксперимента, реализованного по ортогональному центральному композиционному плану (ОЦКП). Ее основными функциями являются: расчет коэффициентов модели; вычисление невязки между данными эксперимента и полученными при использовании модели результатами; сохранение данных в формате, совместимом с остальными двумя; вывод результатов на печать.
В программе имеются органы управления для переключения на подпрограммы построения графиков и пересчета моделей, о которых пойдет речь ниже. Объем программы составляет 7,5 килобайт исходного кода.
Программа позволяет производить расчет коэффициентов как двухфакторных, так и однофакторных моделей.
Программа построения графиков по двухфакторной полиномиальной модели служит для построения кривых для модели вида Y = f(X1, X2) итерационным методом с задаваемой пользователем точностью, что обеспечивает хорошую скорость сходимости. Максимальное количество кривых - 10.
Если программа построения графиков была запущена из OCCP2F, то рассчитанная модель будет автоматически подставлена в соответствующие позиции ввода в Grapher2F, что значительно ускоряет и упрощает работу пользователя с программными продуктами. Объем программного кода - 9,2 килобайта.
Программа построения графиков по полиномиальной модели позволяет строить одиночные кривые и семейство кривых в пределах диапазона измерения, т.е. позволяет проводить интерполяцию и экстраполяцию параметра за пределами измеряемого диапазона - прогнозировать состояние объекта.
На рис. 18.5 представлены графики линейной модели K=f(T,r).
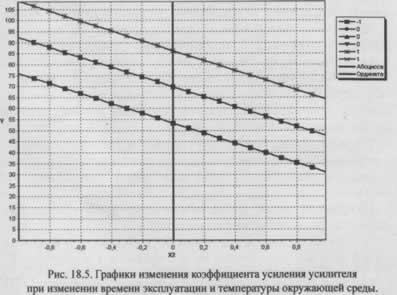
В данном примере задана 5%-ная ошибка эксперимента. Если задать меньшую ошибку, например 2%-ную, все коэффициенты будут значимыми и линейная модель не будет адекватной.
Полученный интерполяционный полином можно использовать для определения значения прогнозируемого параметра Кy.
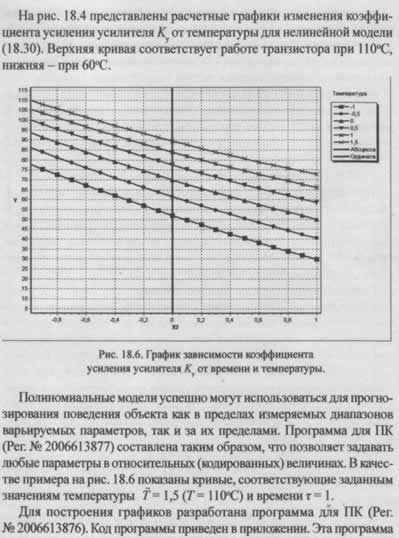
также позволяет строить прогнозирующие полиномы и однофакторные кривые как частный случай двухфакторной модели при b2 - Ь22= Ь12 = 0.
Пример расчета коэффициентов однофакторной модели Y=f(x1) как частный случай двухфакторной модели приведен в приложении 8.
Особенностью применения метода планирования активного эксперимента для прогнозирования технического состояния объектов, зависящих от двух факторов, является появление коэффициентов Ьij -эффектов взаимодействия параметров, которые принципиально не могут быть получены при однофакторном подходе к прогнозированию.

