Автор: Денис Аветисян
Новое исследование предлагает способ упростить анализ сложного поведения квантовых систем, состоящих из множества частиц. Ключом к этому служит изучение временной запутанности — особого вида квантовой связи, проявляющейся во времени, а не в пространстве.
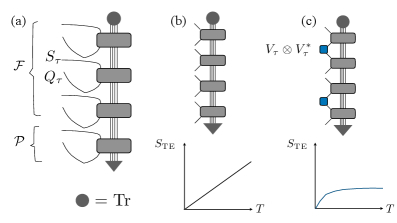
Суть процесса заключается в следующем: создание запутанных состояний (кудитов) и их последовательное взаимодействие с окружающей средой формирует так называемую матрицу влияния. Когда из этой матрицы исключают детали, связанные со средой, происходит удивительный переход. Сложность системы, измеряемая через запутанность, перестаёт расти пропорционально её объёму и начинает подчиняться более простому «закону площади», как только достигается определённый уровень усреднения данных.
Этот переход, называемый коарсенизацией, открывает путь к упрощённому описанию динамики локальных наблюдаемых величин в системе. Получается, что для понимания того, как ведут себя отдельные части сложной системы, не обязательно учитывать всю её внутреннюю запутанность.
В хаотичных квантовых системах локальные наблюдаемые быстро приходят к тепловому равновесию, но общая сложность системы, выраженная через временную запутанность, долгое время оставалась загадкой. Работа «Фазовый переход временной запутанности в хаотичной квантовой многочастичной динамике» исследует связь между этой запутанностью, немарковским поведением (когда система «помнит» своё прошлое) и локальными временными корреляциями. Исследование показывает, что если уменьшить частоту «наблюдений» за системой, проведя грубое усреднение, то масштабирование временной запутанности меняется с объёмного на поверхностное. Это наводит на мысль, что для описания динамики локальных параметров достаточно упрощённой версии матрицы влияния. Возникает фундаментальный вопрос: так ли уж важны сложные временные корреляции, или они являются избыточными для нашего понимания эволюции квантовых систем?
Шёпот Хаоса: Влияние Окружения на Квантовую Динамику
Чтобы понять открытые квантовые системы, нельзя рассматривать их изолированно — необходимо учитывать влияние окружающей среды, или «ванны». Матрица влияния (Influence Matrix) как раз и служит математическим инструментом для описания того, как «ванна» воздействует на исследуемую часть системы — «зонд». Для изучения этих матриц используются различные квантовые модели, такие как схемы со случайными, двойными унитарными или флокетовскими преобразованиями. Всякое предсказание будущего квантовой системы — это не точный расчёт, а скорее попытка договориться с её внутренним хаосом.
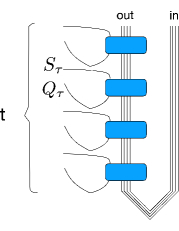
На схеме показано разделение состояния системы: часть относится к «зонду», а часть — к «ванне». Степени свободы «ванны», в свою очередь, делятся на входящие и исходящие. Синие блоки на схеме соответствуют унитарным преобразованиям, описывающим эволюцию системы вперёд во времени.
Временная Запутанность: От Равновесия к Хаосу
Временная запутанность внутри матрицы влияния — это мера того, как информация распространяется и переплетается во времени. Анализ выявил два принципиально разных режима. В простых, упорядоченных динамических режимах запутанность подчиняется «закону площади» (Area Law TE), то есть её сложность растёт пропорционально поверхности некой условной области. В хаотичных же режимах с сильными корреляциями действует «закон объёма» (Volume Law TE), что означает экспоненциально более быстрый рост сложности. Ключевое открытие — наблюдение перехода от закона объёма к закону площади при применении процедуры грубого усреднения данных.
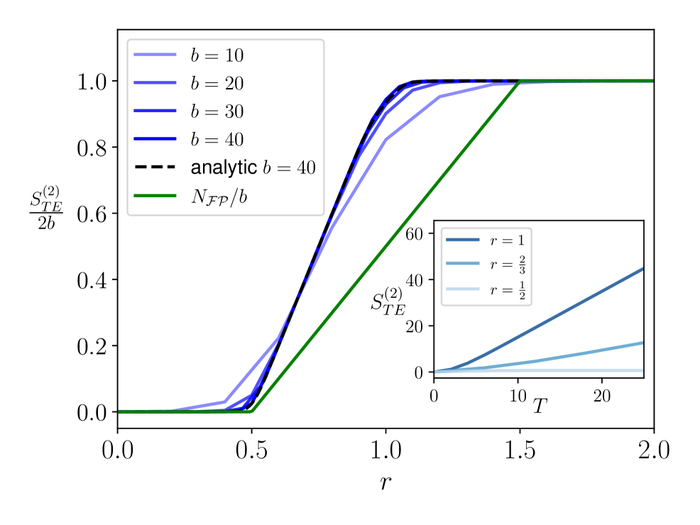
На графике показана максимальная временная запутанность (Rényi-2 TE) для модели случайной унитарной «ванны» в зависимости от параметра. Штриховая линия соответствует аналитическому предсказанию. Главный результат виден на вставке: при уменьшении детализации наблюдений (параметр грубого усреднения) происходит чёткий переход от масштабирования по закону объёма к масштабированию по закону площади.
Упрощение Сложности: Грубое Усреднение и Сжатие
Вычислительная сложность работы с полной матрицей влияния огромна. Метод грубого усреднения (Coarse-Graining) позволяет её значительно снизить. Для дальнейшего «сжатия» квантового состояния используются такие математические методы, как разложение Шмидта (Schmidt Decomposition) и усечение по сингулярным числам (Singular Value Truncation). Полученные в результате компактные представления сохраняют высокую точность, особенно для описания медленно меняющихся наблюдаемых величин. Это подтверждает правомерность закона площади и ставит под сомнение необходимость учёта полного закона объёма. Предложенные методы делают исследование динамики сложных систем вычислительно осуществимым.
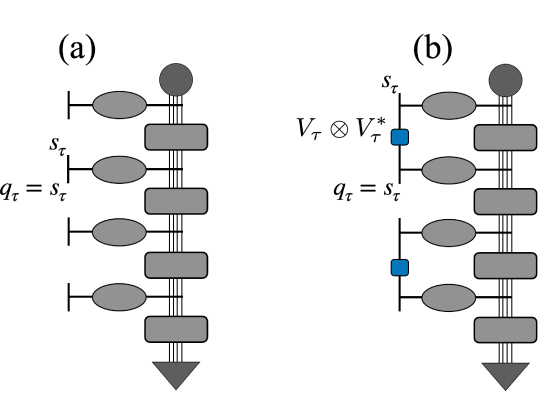
Диаграмма иллюстрирует структуру матрицы влияния ограниченного типа, возникающей при взаимодействии «зонда» и «ванны». Справа показана та же матрица после процедуры грубого усреднения, демонстрирующая её упрощённую, блочную структуру.
Исследование Динамических Систем: Модель Kicked Ising
Для проверки методов на физически значимой системе была выбрана модель Киккого Изинга (Kicked Ising Model), пример флокетовской схемы. Анализ её матрицы влияния позволяет изучать скорость распространения информации в системе, которую характеризует так называемая «скорость бабочки» (Butterfly Velocity). Переход от закона объёма к закону площади был подтверждён не только для абстрактных случайных моделей, но и для этой конкретной физической системы.
Это свидетельствует о том, что сложные мульти-временные корреляции, ответственные за закон объёма, не являются критически важными для описания поведения нескольких временных корреляторов, которые обычно и интересуют физиков.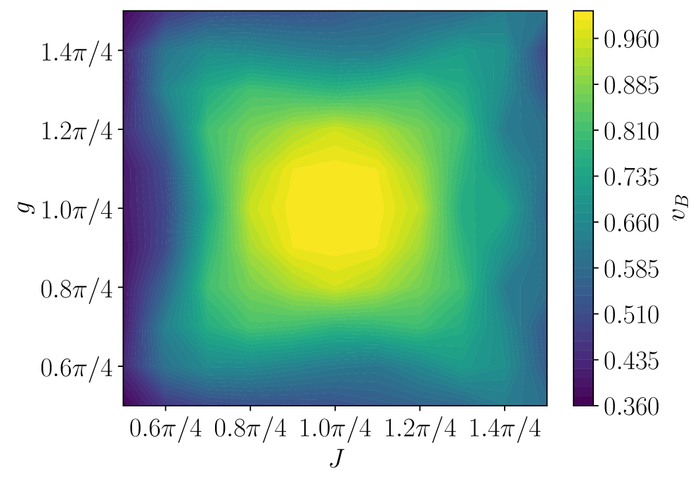
Скорость бабочки vB, извлеченная из фронта вневременной корреляционной функции, составляет L=10.
Вселенная не дискретна, просто у нас недостаточно памяти для чисел с плавающей точкой.
Исследование временной запутанности подтверждает интуитивное предположение: кажущаяся сложность квантового хаоса может быть иллюзией, порождённой избытком деталей. Данные показывают, что грубое усреднение способно «свернуть» закон объёма в закон площади. Это означает, что для описания динамики локальных наблюдаемых сложная временная запутанность может быть несущественной. Как отмечал Луи де Бройль, любое измерение — это вмешательство наблюдателя. В данном случае само «вмешательство» в виде грубого масштабирования упрощает картину, отсекая избыточную информацию. Это не отрицает существование запутанности, но показывает, что её влияние на локальные процессы можно описать гораздо проще. Даже в хаосе можно обнаружить порядок, если смотреть на систему под правильным углом.
Что дальше?
Эта работа вселяет осторожный оптимизм: возможно, хаос можно обуздать, сведя его сложную запутанность к взаимодействиям на границах. Однако не стоит впадать в эйфорию. Грубое усреднение — это не победа над хаосом, а лишь способ приглушить его голос. Остаётся открытым главный вопрос: не скрывается ли истинная динамика системы как раз в тех отброшенных деталях, в том «шуме», который мы так старательно отфильтровываем?
Ключом к разгадке может стать изучение немарковских эффектов — тех «отголосков» прошлого, которые просачиваются даже сквозь грубое усреднение. В конце концов, любое приближение — это компромисс с реальностью, и за каждым упрощением остаётся неучтённый след. Необходимо создать инструменты, способные улавливать эти следы и измерять потерю информации при переходе от полной запутанности к закону площади.
В перспективе важно исследовать, как разные методы грубого усреднения влияют на предсказание поведения конкретных наблюдаемых. Может ли умелое игнорирование части информации привести к новым качественным предсказаниям? Или это лишь иллюзия контроля, за которой последует новый виток сложности? Ответ, как всегда, скрыт в данных — в тихом шёпоте квантовых систем, который нам только предстоит полностью расшифровать.
Оригинал статьи: https://arxiv.org/pdf/2511.03846.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Больше интересных статей здесь: Производство.
Источник статьи: Временная запутанность: от хаоса к порядку.