В этой статье мы начинаем знакомство с математическим анализом — мощным инструментом, который часто используется в физических расчетах. Многие читатели сталкиваются с трудностями при виде интегралов и дифференциальных уравнений, поэтому наша цель — сделать эти концепции понятными и показать их практическую ценность.
Эта статья не является учебником в полном смысле слова. Мы опустим некоторые детали, сосредоточившись на объяснении сути, роли и принципов матанализа, а также на том, как с его помощью решать физические задачи. Рассматривайте этот материал как отправную точку для погружения в тему. Для глубокого изучения рекомендуем обратиться к университетским учебникам, ссылки на дополнительные ресурсы будут приведены в тексте.
В первой части мы рассмотрим следующие ключевые темы:
1. Почему физика требует математического анализа?
2. Что такое функция?
3. Производные и дифференциалы: как решать большие задачи малыми величинами.
4. Интегралы: что это, зачем нужны и какие бывают.
5. Дифференциальные уравнения — функциональные уравнения.
Во второй части мы применим эти знания к конкретным физическим задачам.
Зачем физике матанализ?
Чтобы понять необходимость математического анализа, рассмотрим практические примеры. Возьмем классическую задачу: кубик льда, плавающий в стакане с водой.
1. Статическая часть: Какая часть кубика будет погружена в воду после остановки? Эту задачу может решить семиклассник, зная плотности льда и воды, с помощью закона Архимеда.
2. Динамическая часть: Как будет двигаться кубик после того, как его отпустят? Здесь школьных формул уже недостаточно. Проблема в том, что сила, действующая на кубик (а значит, и его ускорение), зависит от глубины погружения, которая, в свою очередь, меняется со временем. Получается взаимосвязанная система, которую не описать простыми алгебраическими уравнениями. Именно математический анализ предоставляет аппарат для решения таких задач.
Кроме того, матанализ часто предлагает более простые и изящные решения. Например, для расчета силы давления воды на сферический купол можно применить остроумный мысленный эксперимент с «добавлением» воды, но это требует нестандартного подхода. Интегральное же вычисление давления — метод более прямолинейный и систематический, хоть и требует больше вычислений. В целом, производные и интегралы либо упрощают решение, либо делают его вообще возможным.
Что такое функция
Функция — это зависимость одной величины от другой. Более формально, это правило, которое каждому числу (или набору чисел) из одной области ставит в соответствие число (или набор чисел) из другой области. Величины, от которых зависит функция, называются аргументами или параметрами.
Примеры функций в физике:
- Закон равномерного движения: s = v * t. Путь s зависит от скорости v и времени t.
- Закон Ома: I = U / R. Сила тока I зависит от напряжения U и сопротивления R.
- Площадь круга: S = π * r². Площадь S зависит от радиуса r.
График функции наглядно показывает, как меняется ее значение при изменении аргумента.
Что делает математический анализ с функциями?
1. Исследует и преобразует их. Мы можем, зная одну функцию (например, скорость от времени), найти связанную с ней другую (например, пройденный путь). Это похоже на алгебру, где мы преобразуем числа, но здесь мы работаем с целыми зависимостями.
2. Определяет функции из заданных соотношений. Если нам известна связь между функцией и ее производными (например, между ускорением и координатой для пружинного маятника), мы можем найти саму функцию. Для этого служат дифференциальные уравнения.
Таким образом, владея нужной функцией, мы получаем полную информацию о процессе: можем вычислить значение величины в любой момент времени и наоборот.
Производная и дифференциал: как маленькие величины решают большие задачи
Производная функции показывает скорость ее изменения. Рассмотрим мотоциклиста, положение которого на дороге описывается функцией x(t). Тогда производная x'(t) — это его мгновенная скорость. Производная от скорости, в свою очередь, — это ускорение. В электротехнике производная заряда по времени дает силу тока.
Формальное определение: Производная — это предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
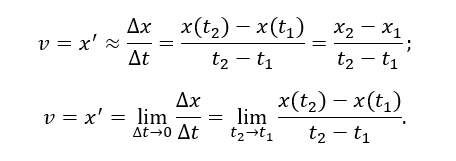
На графике это соответствует угловому коэффициенту касательной к графику функции в данной точке. Чем ближе мы берем две точки на кривой, тем больше отрезок между ними похож на прямую — касательную.
Дифференциал — это бесконечно малое изменение функции (dx) или аргумента (dt). Производную можно записать как отношение дифференциалов: dx/dt. С дифференциалами можно работать как с обычными числами: умножать, делить, что активно используется при решении физических задач (например, при выводе закона сохранения энергии для маятника).
Рассмотрение процессов через бесконечно малые приращения — ключевой метод решения многих физических проблем.
Что такое интеграл, зачем он нужен и каким бывает
Интеграл — операция, обратная дифференцированию. Если проинтегрировать функцию, а потом продифференцировать результат, получится исходная функция.
Два основных взгляда на интеграл:
1. Сумма бесконечно малых величин. Например, чтобы найти силу давления воды на стенку сосуда, где давление меняется с глубиной, мы мысленно разбиваем стенку на бесконечно тонкие горизонтальные полоски. На каждой полоске давление почти постоянно. Вычисляем малую силу для каждой полоски и суммируем (интегрируем) их, чтобы получить полную силу.
2. Площадь под графиком. Определенный интеграл функции на отрезке численно равен площади фигуры под ее графиком. Этот подход также основан на суммировании площадей бесконечно узких прямоугольников.
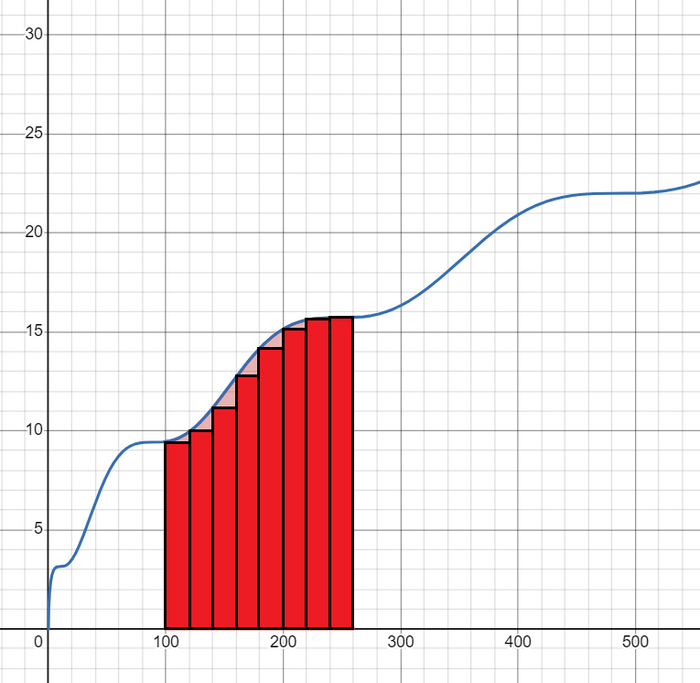
Виды интегралов:
- Неопределенный интеграл — это семейство первообразных функций.
- Определенный интеграл — это число, равное разности значений первообразной на границах интервала.
Интегралы, как и производные, позволяют преобразовывать функции: из ускорения получить скорость и координату, из силы тока — заряд, из распределения давления — полную силу.
Помимо обычных, существуют и более сложные интегралы:
- Двойные и тройные — для интегрирования по площади и объему (например, для нахождения массы неоднородного тела).
- Криволинейные — вдоль заданной линии (например, для расчета работы силы вдоль траектории).
- Поверхностные — по заданной поверхности (например, для вычисления потока векторного поля).
Дифференциальные уравнения - уравнения для функций
Дифференциальные уравнения (ДУ) — это уравнения, в которых неизвестной является не число, а функция. В них могут входить как сама искомая функция, так и ее производные различных порядков.

Именно такие уравнения описывают большинство физических законов: движение тел под действием сил, рост популяций, электрические цепи и многое другое.
Классификация ДУ:
- Обыкновенные (искомая функция зависит от одного аргумента) и в частных производных (функция зависит от нескольких аргументов).
- Порядок уравнения определяется порядком старшей производной.
- Линейные и нелинейные.
Как решать ДУ? Существуют аналитические методы (разделение переменных, замена, и т.д.) для многих типов уравнений. Однако большинство реальных физических уравнений не имеют простого аналитического решения и решаются численными методами на компьютере.
На этом наш краткий обзор основ математического анализа завершен. В следующей части мы применим эти инструменты к решению конкретных задач классической физики.
Желаем успехов в освоении этого увлекательного раздела математики!
Обратите внимание: MIT: ядерная энергия является неотъемлемой частью будущего энергетики с низким содержанием углерода.
Больше интересных статей здесь: Новости науки и техники.
Источник статьи: Как понять матанализ и решать им задачи классической физики | Часть 1.

