В практических задачах оптимизации параметры настройки часто имеют допустимые границы, что требует модификации классических алгоритмов. Симплекс-метод, представляющий собой итерационную процедуру движения многомерной геометрической фигуры (симплекса) по поверхности отклика, должен учитывать эти ограничения. Рассмотрим, как происходит движение симплекса, когда одно из значений параметра (например, x1) выходит за допустимые пределы.
Процедура настройки с учётом ограничений
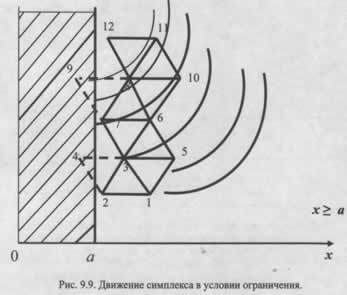
На начальном этапе проводятся опыты в вершинах исходного симплекса (точки 1, 2, 3). После сравнения результатов определяется наихудшая точка (в данном случае — точка 1). Согласно стандартной процедуре, её следует отразить относительно противоположной грани (2-3), чтобы получить новую точку 4. Однако, если вычисленная точка 4 оказывается за пределами реализуемой области (например, при x1 < x1_min), этот шаг невозможен.
В такой ситуации алгоритм адаптируется: вместо отражения недопустимой точки производится отражение следующей наихудшей точки из оставшихся вершин симплекса (точка 2). Это приводит к точке 5. Далее процесс продолжается: отражается точка 1, получается точка 6, и так далее. Если и эта новая точка (например, точка 9 как отражение точки 6) нарушает ограничение, процедура повторяется — находится следующая наихудшая точка (7), отражается в точку 10, затем снова отражается точка 6. Таким образом, симплекс, «отталкиваясь» от границы допустимой области, продолжает движение в сторону оптимальных значений параметров настройки, обходя ограничения.
Универсальность метода и геометрическая интерпретация
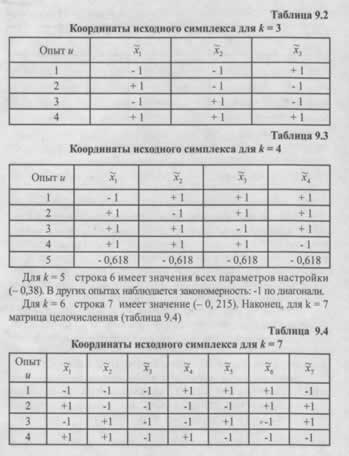
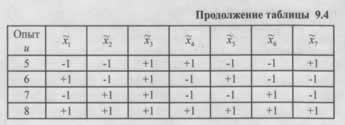
Для практического применения метода разработаны таблицы с координатами исходных симплексов при настройке по трём и четырём параметрам (Таблицы 9.2-9.3). Ключевой особенностью является представление координат в безразмерных, относительных единицах. Этот подход обеспечивает универсальность: одни и те же симплексы размерности от k=2 до k=7 могут использоваться для оптимизации систем самой разной физической природы — от химических процессов до инженерных систем.
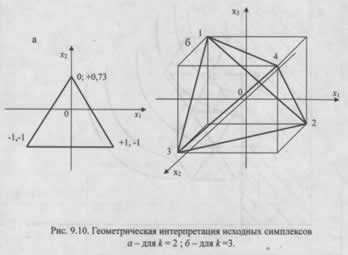
Геометрически симплекс — это простейшая фигура в k-мерном пространстве, состоящая из (k+1) вершин. Например, для трёх параметров (k=3) симплекс представляет собой тетраэдр (пирамиду с треугольным основанием). Наглядная иллюстрация такого трёхмерного симплекса помогает понять принцип его движения в пространстве параметров.
Достоинства и недостатки последовательного симплекс-метода (ПСМ)
Существует множество модификаций ПСМ, направленных на ускорение сходимости. Однако важно отметить, что эти усложнённые версии часто проигрывают классическому ПСМ в простоте применения и не всегда демонстрируют преимущество в решении конкретных задач.
Последовательный симплекс-метод обладает рядом значительных преимуществ:
- Адаптивность к изменяющимся условиям. В реальных процессах (например, в судовых системах) оптимальные параметры могут со временем смещаться. ПСМ, принимая решения на основе последних (k+1) экспериментов, эффективно «следит» за таким движущимся оптимумом, компенсируя погрешности измерений.
- Чёткость и масштабируемость. Метод даёт однозначные инструкции по изменению условий процесса. Его алгоритм хорошо формализован, не усложняется с ростом числа факторов и даже становится более эффективным при увеличении размерности задачи.
- Простота реализации. Для работы метода не требуется вычислять направление наискорейшего подъёма или проводить сложный статистический анализ. Расчёт новых точек сводится к базовым арифметическим операциям. Это позволяет использовать ПСМ как с помощью ЭВМ, так и вручную.
- Работа с качественными и множественными откликами. Для определения направления движения достаточно качественно сравнить результаты опытов и выявить наихудший. Это позволяет применять ПСМ, когда отклик оценивается качественно, а не измеряется количественно, а также при наличии нескольких целевых параметров. Метод не предъявляет жёстких требований к «правильности» формы симплекса, допуская использование нерегулярных конфигураций.
- Гибкость. На любом этапе эксперимента можно легко добавить новый варьируемый параметр, введя всего одну дополнительную точку, которая расширит текущий симплекс до большей размерности.
- Психологический комфорт для экспериментатора. Решение о следующем шаге принимается после каждого опыта, а не после целой серии. Это снижает вероятность необходимости проведения заведомо «плохих» экспериментов, предусмотренных жёстким планом.
К основному недостатку ПСМ можно отнести:
- Ограниченность информации о поверхности отклика. Движение по правилам симплекса даёт лишь локальную информацию и не позволяет построить полную модель или глубоко изучить глобальную структуру поверхности отклика в области исследования.

