Введение: Две силы в процессе эксплуатации
В процессе эксплуатации сложных радиоэлектронных систем и средств автоматики происходят два противоположных типа процессов. С одной стороны, действуют деградационные процессы, которые постепенно ухудшают состояние системы, снижая её безотказность и выводя рабочие параметры за пределы допустимых норм. С другой стороны, им противостоят стабилизирующие процессы, задача которых — сопротивляться деградации, поддерживать работоспособность системы и восстанавливать её техническое состояние.
Что относится к стабилизирующим процессам?
К стабилизирующим процессам можно отнести как автоматические механизмы, встроенные в систему (например, автоматическую регулировку усиления (АРУ) или автоподстройку частоты (АПЧ)), так и ручные или полуавтоматические операции, выполняемые в ходе технического обслуживания и ремонта. К последним относятся различные подстройки и регулировки параметров, возникающие после замены элементов.
Сложность процесса настройки
Процесс настройки объекта на оптимальный режим работы часто представляет собой нетривиальную задачу, особенно когда требуется одновременно настроить два или более параметра. Для её решения необходимы специальные знания и методы. В основе задачи лежит поиск таких значений настраиваемых параметров (обозначим их как xi), при которых выбранный показатель качества работы системы (J) достигает своего экстремального (наилучшего) значения — максимума или минимума. Зависимость J от параметров обычно имеет экстремум, но его точное положение заранее неизвестно.
Простой случай: настройка одного параметра
Рассмотрим самый простой вариант, когда количество настраиваемых параметров k = 1. В этом случае параметром настройки (x) может быть, например, сопротивление резистора, ёмкость конденсатора или положение ручки потенциометра, выраженное в соответствующих единицах (Ом, мкФ, градусы).
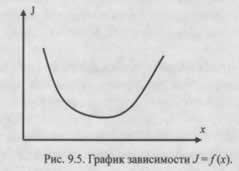
На Рисунке 9.5 показана типичная зависимость показателя качества J от параметра x. Проведя эксперимент в одной точке и выбрав шаг изменения параметра, можно определить направление движения к оптимуму. Для этого достаточно провести дополнительный эксперимент в соседней точке. Ситуация кардинально усложняется при переходе к настройке двух и более параметров.
Методы оптимизации для нескольких параметров
Для решения задач многопараметрической оптимизации рекомендуется использовать методы, основанные на теории планирования эксперимента. Эта теория предоставляет специалистам несколько эффективных алгоритмов поиска оптимальных соотношений параметров как в статике, так и в динамике. Среди них:
- Метод крутого восхождения (движение по градиенту).
- Метод эволюционного планирования Бокса.
- Метод последовательного симплексного планирования и его модификации.
Последовательный симплекс-метод (ПСМ) — оптимальный выбор
Для настройки радиоэлектронного оборудования (РЭО) и средств автоматики (СА) наиболее подходящим считается метод последовательного симплексного планирования (ПСМ). Его ключевые преимущества — относительная простота и высокая устойчивость к внутренним и внешним помехам, что особенно важно при работе с судовыми и другими сложными объектами.
Принцип работы симплекс-метода
Основная идея метода заключается в работе с геометрической фигурой, называемой симплексом. В пространстве с k параметрами (факторами) симплекс представляет собой фигуру, образованную k+1 точкой, равноудалёнными друг от друга. Например:
- Для одного параметра (k=1) симплекс — это отрезок прямой.
- Для двух параметров (k=2) — равносторонний треугольник.
- Для трёх параметров (k=3) — правильный тетраэдр.
Для большего числа параметров геометрическое представление теряет наглядность, но математический аппарат остаётся рабочим.
Процесс "кантования" симплекса
Поиск оптимума осуществляется путём последовательного перемещения ("кантования") симплекса по поверхности отклика (графику функции качества J). Алгоритм на каждом шаге выглядит так:
- В вершинах текущего симплекса проводятся опыты (измерения показателя J).
- Определяется вершина с наихудшим результатом.
- Эта вершина зеркально отражается относительно противоположной грани симплекса, формируя координаты новой точки.
- В новой точке ставится опыт, и наихудшая вершина заменяется на эту новую, образуя следующий симплекс.
- Процесс повторяется, постепенно смещая симплекс в область лучших значений показателя качества.
Наглядный пример для двух параметров
На Рисунке 9.6 показан порядок постановки опытов при симплексном планировании для двух факторов. Исходный симплекс — треугольник с вершинами 1, 2, 3. Предположим, наихудший результат в точке 1.
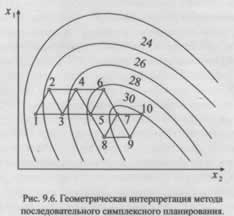
Симплекс "переворачивается" через грань 2-3, и в новой точке 4 ставится опыт. Далее анализируются результаты в точках 2, 3, 4, определяется новая наихудшая вершина, и процесс кантования продолжается (например, поворот через грань 3-4 в точку 5 и т.д.).
Начало и завершение процесса оптимизации
Процедура начинается с выбора исходного симплекса. Чем больше его размер, тем быстрее начальное продвижение к оптимуму. По мере приближения к цели размер симплекса можно уменьшать для более точной настройки.
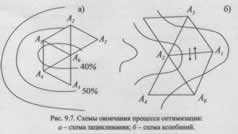
О завершении процесса оптимизации сигнализируют два характерных признака (Рисунок 9.7):
- Зацикливание — симплекс начинает вращаться вокруг одной вершины.
- Колебание — вершина симплекса колеблется относительно одной грани.
Математическое обеспечение метода
Координаты новой вершины симплекса после отражения рассчитываются по общей формуле:
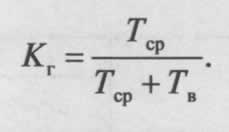
где N = k + 1 — количество точек в исходном симплексе; Xj, N+1 — координата новой точки для фактора с номером j в натуральных величинах; X*j — координата этого же фактора в отвергнутой (наихудшей) точке.

Таким образом, последовательный симплекс-метод представляет собой мощный и практичный инструмент для точной и надёжной настройки сложных систем, напрямую влияя на повышение их эксплуатационной надёжности.

