Это перевод третьей статьи из серии расследований Data Colada о фальсификации данных в статьях профессора Гарвардской школы бизнеса Франчески Джино.
Первую часть можно прочитать здесь, вторую здесь.
Напоминаю, что этот пост — мой вольный пересказ опроса Data Colada; Все картинки оттуда.
Пойдем.
Часть 3: Мошенники не при делах
На этот раз речь пойдет о статье Джино и Вильтермута «Злой гений? Как нечестность может привести к большему творчеству» «Злой гений? Как нечестность может привести к большему творчеству», опубликованной в 2014 году, в частности об исследовании 4.
Авторы исследования Data Colada уточняют, что, по имеющейся у них информации, соавтор Джино не выполнял и не помогал в сборе данных для рассматриваемого эксперимента. База данных была получена несколько лет назад напрямую от профессора Джино.
Что ты учишь?
Эксперимент проводился онлайн. Участники (178 человек) сначала выполнили задание, где подбрасывали виртуальную монету и где можно было схитрить. Затем участникам было предложено два творческих задания. Далее остановимся на результатах задания «использование», где задача заключалась в том, чтобы за 1 минуту придумать как можно больше творческих способов использования газеты (ранее это задание использовалось другими исследователями как способ оценки креативности).
Что ты получил?
Гипотеза авторов подтвердилась: участники, обманувшие при подбрасывании монеты, придумали больше вариантов использования газеты (M = 8,3, SD = 2,8), чем участники, не обманывавшие (M = 6,5, SD = 2,3, p<0,0001).
Но опять аномалия: неупорядоченные наблюдения
Как и в первой части расследования, фатальный признак подлога связан с сортировкой данных.
База данных практически идеально отсортирована на две колонки: сначала по колонке «обманули», указывающей, списывали ли участники в задании на подбрасывание монеты (0 — не списывали; 1 — списывали), а затем по колонке «Количество ответов», в котором указано, сколько вариантов использования газеты придумал участник.
Как и в случае с первым опросом, тот факт, что сортировка почти идеальна, раздражает весь офис.
Давайте посмотрим, как сортируются данные. На скриншоте ниже показаны первые 40 наблюдений. Поскольку данные сначала сортируются по столбцу «мошенничество», все эти наблюдения представляют НЕ-мошенников, которые, соответственно, имеют 0 баллов в этом столбце. А потом они прекрасно сортируются по столбцу «Количество откликов» — всего 135 человек.
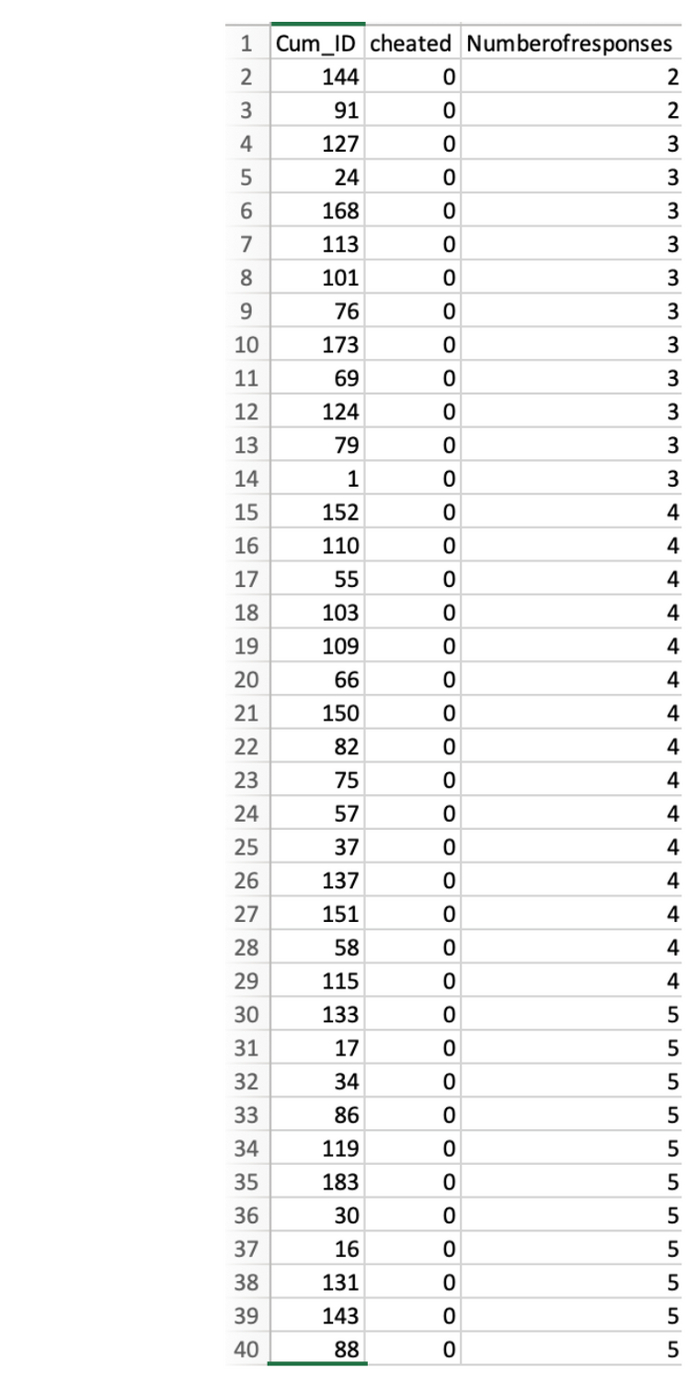
Теперь давайте посмотрим на мошенников.
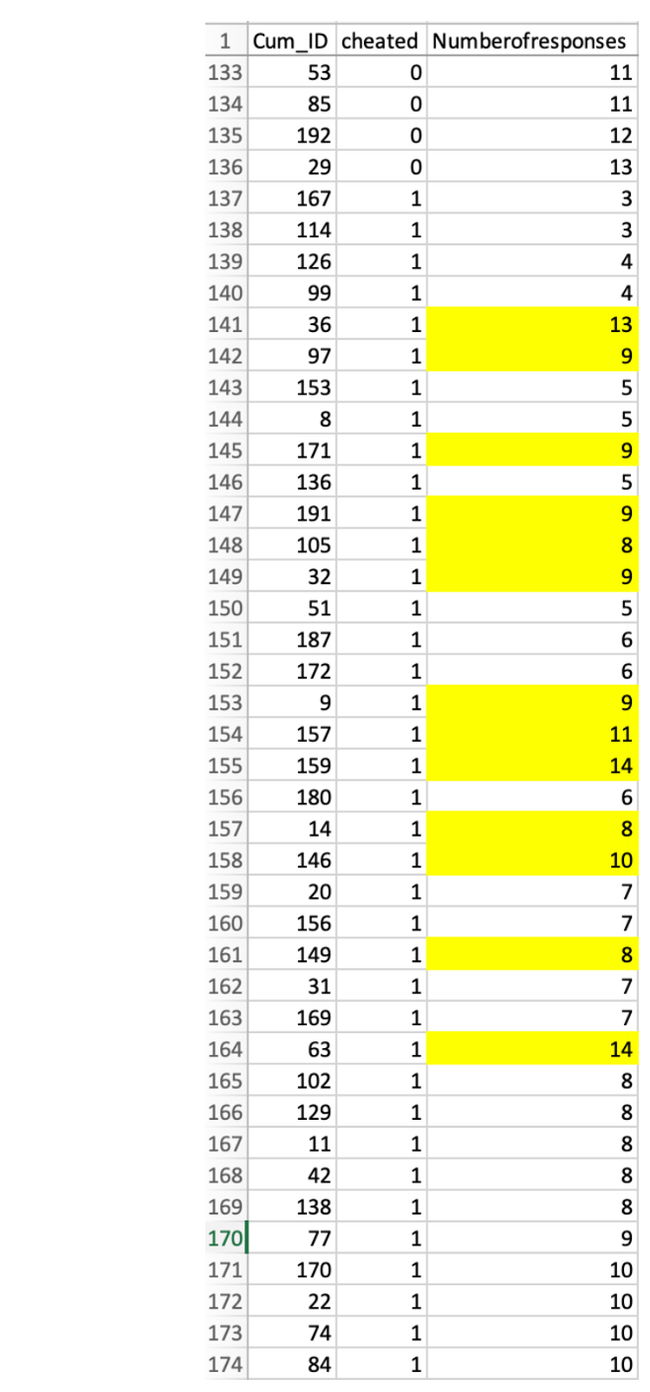
о нет: хотя 43 самозванца тоже отсортированы по количеству ответов, среди них есть 13 наблюдений, которые расположены не в том порядке, в котором должны быть.
Это дает основания подозревать, что эти 13 наблюдений были вручную изменены после сортировки для достижения желаемого эффекта.
Здесь нужно отметить три важные вещи
1. Невозможно отсортировать набор данных таким образом, чтобы получить порядок размещения данных, либо они были изначально введены таким образом (что маловероятно, поскольку данные изначально были файлом Qualtrics [онлайн-исследовательская платформа] которые по умолчанию отсортированы по времени), или они были изменены вручную.
2. Помните, что строки отсортированы по столбцу «Количество ответов». Если неупорядоченные значения были изменены, легко определить, какими они были изначально. Например, в строке № 141 есть «13». Строка выше имеет «4», а первое значение после нее — «5». Следовательно, если данные были изменены, можно предположить, что это «13» раньше было либо «4», либо «5».
3.
Обратите внимание: MIT: ядерная энергия является неотъемлемой частью будущего энергетики с низким содержанием углерода.
Появится немного дольше, но сначалаПопробуем угадать, как выглядели исходные данные
Ниже вы можете увидеть два новых столбца — расчетный минимум и расчетный максимум, в которых есть два оценочных значения. В некоторых случаях точно известно, какое число изменилось, в некоторых — в пределах ±1.
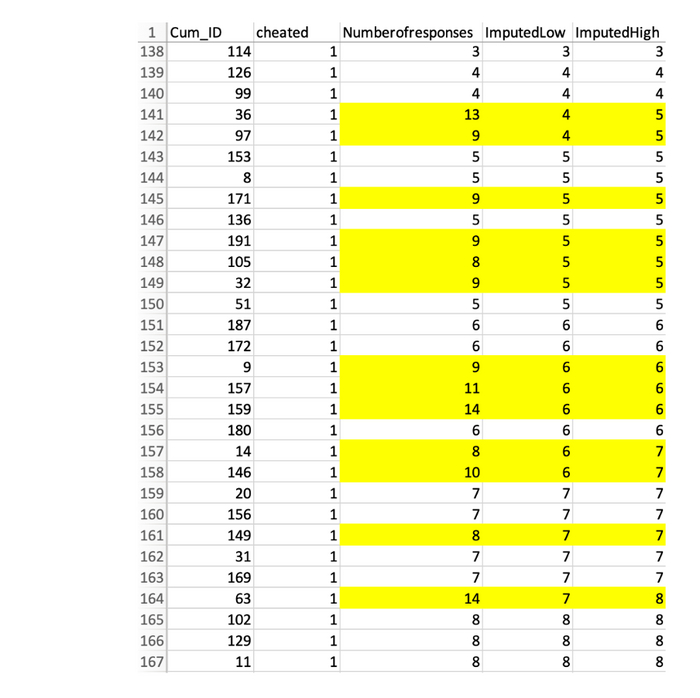
Давайте посмотрим, есть ли отличия между опубликованным набором данных (слева) и предполагаемым реальным (справа) на графиках:
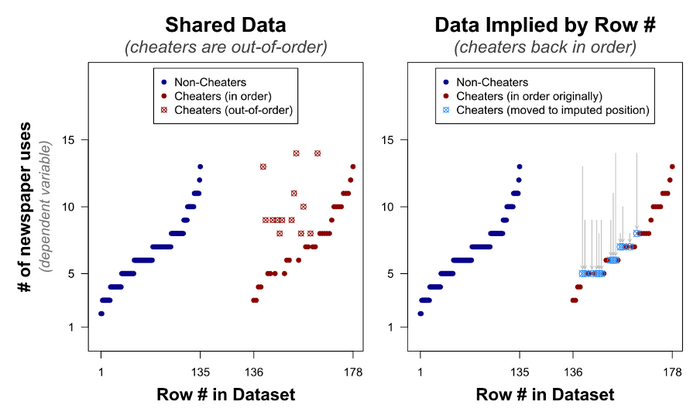
И добраться до сути
3. Существенная связь между читерством и творчеством исчезает, когда анализируешь якобы настоящие ценности, а не те, которые выложили Джино и соавтор. Значение p колеблется от <0,0001 до 0,292 (для оценочных минимальных значений) и p = 0,180 (для оценочных максимальных значений).
Это
Если бы значения не менялись вручную, не было бы существенной разницы между мошенниками и немошенниками.
Для интересующихся будет более хардкорный анализ
Представьте себе, что на самом деле нет никакой разницы между мошенниками и обычными мошенниками в их способности понять, как пользоваться бумагой.
При отсутствии фальсификации данных мы ожидаем, что не только среднее количество ответов будет одинаковым, но и общие распределения для обеих групп будут схожими. Например, значение, которое находится в 20-м процентиле, должно быть одинаковым как для мошенников, так и для не-мошенников. И это также относится к 50-му процентилю, 80-му, 90-му и так далее.
Что ж, давайте посмотрим на распределение обеих групп по поддельным (слева) и предположительно реальным (справа).

Критерий Колмогорова-Смирнова для непараметрического сравнения целочисленных распределений показывает p = 0,456, что не позволяет отвергнуть гипотезу о том, что эти два распределения равны (то есть равны).
Хорошо, но насколько впечатляет этот нулевой балл? Принято как доказательство того, что 13 наблюдений, «возвращенных к реальности», на самом деле были сфальсифицированы.
Но, возможно, это неправда. Может быть, неважно, какие 13 наблюдений вы меняете? Что, если вы измените любые другие 13 наблюдений (из мошеннической группы) на ту же сумму? Получим ли мы такие же равные распределения и, например, такое же высокое значение p в тесте Колмогорова-Смирнова?
Краткий ответ: нет.
Data Colada запускала несколько консервативных симуляций миллион раз. Каждый раз сходство между читерами и не читерами оценивалось с помощью теста Колмогорова-Смирнова и отслеживалось p-значение.
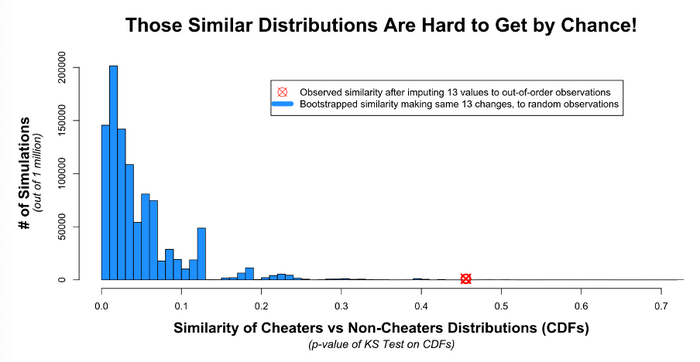
Посмотрите на красную точку, которая представляет p-значение после изменения 13 наблюдений. Вам должно быть невероятно, невероятно повезло, чтобы выбрать именно их и получить такие похожие групповые распределения чисто случайно.
Это
Не существует (почти) другого набора из 13 значений, которые можно изменить на одинаковую величину, чтобы получить два похожих распределения. Этот результат довольно убедительно подтверждает правильность определения поддельных ячеек и их начальных значений.
Комментарий от Data Colada
«Мы считаем, что Гарвардский университет имеет доступ к файлу Qualtrics, что может полностью подтвердить (или опровергнуть) наши опасения. Мы сказали им, какой файл получить, какие ячейки проверить и какие значения они найдут в файле Qualtrics, если бы мы были правы. Мы не знаем, сделали ли они это, и что они узнали, если бы сделали. Все, что мы знаем, это то, что 16 месяцев спустя они потребовали отозвать статью».
Спасибо за чтение.
Четвертая часть расследования еще не вышла, но мы ее очень ждем!
Больше интересных статей здесь: Новости науки и техники.
Источник статьи: Большой скандал в научном мире прямо сейчас. Часть 3.

