
Эффект бабочки — это яркая метафора, описывающая фундаментальный научный принцип. Представьте, что взмах крыльев бабочки в одном регионе планеты через цепь взаимосвязанных событий способен инициировать ураган на другом её конце. Эта образная иллюстрация отражает суть явления: ничтожно малые изменения в начальных условиях сложной системы могут привести к колоссальным и совершенно непредсказуемым последствиям в долгосрочной перспективе. Концепция получила широкое признание благодаря работам метеоролога Эдварда Лоренца.
История открытия: от погодных моделей к теории хаоса
Эдвард Лоренц, создавая математические модели для прогнозирования погоды, совершил ключевое наблюдение. В 1961 году, проводя вычисления на одной из ранних ЭВМ, он решил повторить предыдущий расчёт, введя исходные данные не с шестью знаками после запятой, а с тремя. Казалось бы, незначительное округление числа с 0.506127 до 0.506 не должно было серьёзно повлиять на результат. Однако итоговый прогноз погоды оказался кардинально иным. Это открытие легло в основу понятия «чувствительность к начальным условиям» — краеугольного камня теории хаоса.
Научная сущность явления
В строгом научном смысле эффект бабочки — это проявление высокой чувствительности динамической системы к малейшим вариациям стартовых параметров. Динамическая система — это любая система, состояние которой меняется со временем (погода, биологическая популяция, экономика). Из-за этой сверхчувствительности долгосрочное поведение таких систем становится принципиально непредсказуемым, что объясняет, например, сложности с точными метеопрогнозами более чем на 10 дней. Бесчисленное множество мельчайших, неучтённых факторов может накапливаться и полностью менять сценарий развития событий.
Сферы проявления эффекта бабочки
Этот феномен наблюдается далеко за пределами метеорологии, во множестве сложных систем:
— Метеорология и климатология: Классическая область. Минимальный сдвиг температуры, давления или направления ветра в одной точке может через несколько дней или недель привести к формированию или исчезновению мощного циклона за тысячи километров.
— Экономика и финансы: Финансовые рынки — живой пример хаотической системы. Одно неосторожное заявление политика, неожиданная новость компании или даже слух могут вызвать цепную реакцию, приводящую к обвалу или росту индексов.
— Биология и экология: Исчезновение или, наоборот, вспышка численности одного вида (например, насекомого-опылителя) может каскадно повлиять на растения, хищников и всю пищевую цепь, трансформируя экосистему.
— Социальные науки и история: Незначительное событие или решение отдельного человека (опоздание, случайная встреча) иногда становится спусковым крючком для масштабных социальных движений, революций или изменений в культурных трендах.
Математическое моделирование хаоса
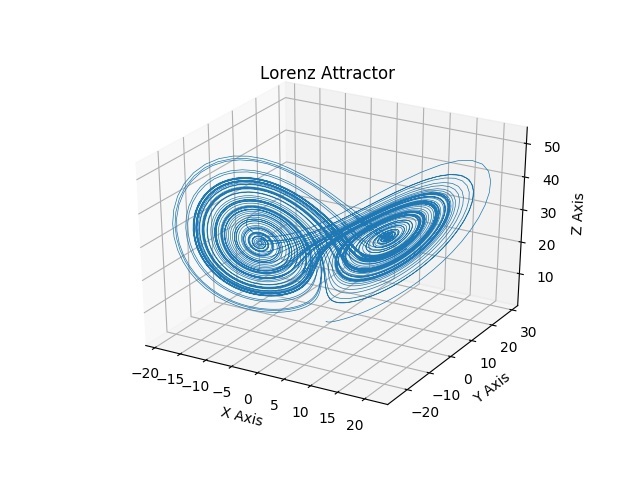
Изучение эффекта бабочки тесно связано с компьютерным моделированием. Лоренц использовал систему из трёх нелинейных дифференциальных уравнений для описания конвекции в атмосфере. Его знаменитый график решений, напоминающий крылья бабочки (аттрактор Лоренца), наглядно показал, как траектории системы, начавшиеся в бесконечно близких точках, со временем радикально расходятся. Это доказывает, что точные долгосрочные прогнозы в хаотических системах принципиально невозможны.
Значение и практическая важность концепции
Эффект бабочки имеет фундаментальное значение для современной науки.
Обратите внимание: Почему смартфон быстро разряжается, что делать.
Он учит нас смирению, показывая пределы предсказуемости сложного мира. Эта концепция заставила пересмотреть подходы к прогнозированию в метеорологии, экономике и социологии, сместив фокус с поиска идеально точного долгосрочного прогноза на анализ сценариев, оценку рисков и повышение устойчивости систем. Она является центральным элементом теории хаоса, которая находит применение в самых разных областях — от астрофизики до нейробиологии.Дополнительные материалы для изучения
Для тех, кто хочет глубже погрузиться в тему эффекта бабочки и теории хаоса, рекомендуем следующие научные работы:
1. Лоренц Э. Н. «Детерминированный непериодический поток» (1963). — Первоисточник, в котором Лоренц впервые описал хаотическое поведение в простой математической модели атмосферной конвекции.
2. Хилборн Р.К. «Хаос и нелинейная динамика: введение для ученых и инженеров» (2000). — Отличный учебник, подробно и строго разъясняющий математические основы хаоса с множеством примеров.
3. Глейк Дж. «Хаос: Создание новой науки» (1987). — Увлекательная научно-популярная книга, рассказывающая историю становления теории хаоса и её ключевых героев доступным языком.
В наших следующих публикациях мы подробнее рассмотрим, как принципы теории хаоса, включая эффект бабочки, помогают понимать устройство и поведение сложных систем вокруг нас.
Больше интересных статей здесь: Новости науки и техники.
Источник статьи: Эффект бабочки: что это и почему он важен?.

