Поиск неисправностей в технических системах может осуществляться с использованием аппаратных или программных средств. В основе этого процесса лежат два ключевых подхода: комбинационный и последовательный методы тестирования, аналогичные применяемым при функциональном диагностировании.
Основные подходы к тестированию
При комбинационном методе анализируется только итоговая комбинация результатов всех выполненных элементарных проверок. Порядок их проведения не имеет решающего значения. Последовательный метод, напротив, предполагает анализ результата каждого теста сразу после его выполнения. Этот метод, в свою очередь, делится на два типа:
- Упорядоченное тестирование: элементарные проверки выполняются в строго заданной, заранее определённой последовательности.
- Условное (адаптивное) тестирование: выбор следующего теста напрямую зависит от исхода предыдущего, что делает процесс более гибким и целенаправленным.
Области применения и критерии оптимизации
Комбинационный метод наиболее эффективен в ситуациях, когда возможны множественные отказы, например, при вводе устройства в эксплуатацию или во время аварийных ситуаций. Последовательный метод чаще применяется при внезапном отказе в процессе штатной работы, когда высока вероятность неисправности лишь одного элемента системы.
Эффективность системы диагностирования, реализуемой программно, оценивается по различным критериям. Оптимальной может считаться система с минимальным временем тестирования, наименьшими требованиями к объёму памяти, минимальной трудоёмкостью проведения проверок или же по комбинированному экономическому показателю, учитывающему несколько факторов.
Метод Шеннона-Фано для построения квазиоптимальных тестов
Этот метод применяется для поиска одиночной неисправности (например, постоянного логического «0» или «1»). Каждой потенциальной неисправности присваивается вероятность её возникновения (p_i), причём сумма всех вероятностей равна 1. Эти вероятности можно оценить методами расчёта надёжности.
Алгоритм построения теста заключается в последовательном разделении множества возможных неисправностей на подмножества. Первый тест выбирается так, чтобы он разделил все неисправности на две группы с примерно равными суммарными вероятностями. По результату теста определяется, в какой из групп находится реальная неисправность. Затем процесс повторяется для выбранного подмножества: выбирается следующий тест, который делит его на приблизительно равновероятные части, и так далее — до тех пор, пока неисправность не будет локализована с требуемой точностью.
Рассмотрим пример на основе таблицы покрытий тестов, где все 14 неисправностей считаются равновероятными.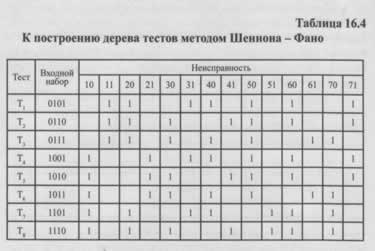
В качестве первого шага выбирается тест Т1. В зависимости от его исхода (обнаружена неисправность или нет) все возможные неисправности делятся на два подмножества: {10,21,30,41, 51,61,70} и {11, 20,31,40, 50, 60,71}.
Предположим, тест Т1 не обнаружил неисправность. Значит, она находится в первом подмножестве. Следующим может быть выбран тест Т3, который разделит это подмножество на {10,21, 41, 51} и {30, 61, 70}.
Таким образом строится полное диагностическое дерево (см. рис. 16.6), позволяющее идентифицировать конкретную неисправность из 14 возможных всего за 3-4 теста. Метод Шеннона-Фано является ярким примером зондовой (адаптивной) организации тестирования, где каждый следующий шаг зависит от результатов предыдущих.
Декомпозиция сложных объектов
При диагностировании сложных логических схем для упрощения задачи часто применяют декомпозицию — разделение объекта на более простые, функционально законченные подсистемы, желательно с одним выходом каждая.
Такой подход позволяет применять методы диагностирования (в том числе и метод Шеннона-Фано) к отдельным модулям, что значительно повышает эффективность поиска неисправностей в крупных и сложных системах.

