Задача прогнозирования и подходы к её решению
В практике прогнозирования технического состояния различных объектов часто возникает необходимость определить момент времени, когда контролируемый параметр достигнет предельного или заранее заданного значения. Эту важную инженерную задачу можно решить несколькими способами: графическим методом или с помощью итерационного алгоритма для вычисления коэффициентов полинома вида r = f(Y, x). Для реализации последнего подхода может быть использована специализированная программа для перестроения двухфакторной модели.
Статистическая обработка и сложности преобразования моделей
Полиномиальные модели, построенные на основе экспериментальных данных, обязательно проходят этап статистической обработки. Этот этап включает в себя сравнительный анализ результатов, полученных по модели, и реальных экспериментальных данных. Важно понимать, что наличие или отсутствие конкретного коэффициента в итоговой модели часто носит случайный характер. Из-за этой стохастической природы прямое преобразование модели с целью выделения управляющего параметра процесса (например, путём решения квадратного уравнения) может привести к некорректным или нестабильным результатам.
Эффективным выходом из этой ситуации является применение итерационных численных методов для нахождения корней уравнения с использованием вычислительной техники (ЭВМ). Такой подход позволяет корректно построить преобразованную математическую модель, избегая аналитических трудностей.
Преобразование двухфакторных полиномиальных моделей
Рассмотрим практический пример преобразования для случая двухфакторных моделей. Допустим, в результате экспериментальных исследований был получен полный квадратичный полином, который адекватно описывает результаты испытаний.
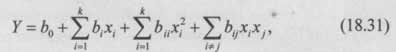
В этом полиноме:
x₁ — это варьируемые в эксперименте параметры, представленные в относительных (кодированных) величинах. Любой из этих факторов может быть интерпретирован как фактор времени.
Y — один из выходных параметров, который регистрируется в процессе контроля состояния объекта.
Постановка задачи: необходимо найти зависимость одного из воздействующих факторов xᵢ от выходного параметра Y и другого варьируемого параметра xⱼ.



Заключение о трудоёмкости и автоматизации
Процесс преобразования полиномиальной модели, как видно из примеров, требует применения итерационных методов для нахождения корней квадратичного полинома. Выполнение этих расчётов вручную является крайне трудоёмкой задачей. Использование специально разработанного программного обеспечения не только существенно облегчает труд исследователя, сокращая время обработки данных, но и открывает новые возможности для анализа сложных моделей, повышая точность и надёжность прогнозов технического состояния.

