Вероятностное прогнозирование представляет собой метод оценки будущего состояния технической системы (ТС) на основе статистических данных. Его суть заключается в определении закона распределения ключевого параметра системы и расчёте вероятности того, что в прогнозируемый период этот параметр останется в допустимых пределах или выйдет за их границы.
Область применения
Данный подход особенно востребован в ситуациях, когда изменение контролируемого параметра e(t) системы носит сложный, стохастический характер, и его поведение трудно описать детерминированными моделями.
Реализация в эксплуатации
При эксплуатации радиоэлектронного оборудования (РЭО) и систем автоматики (СА) вероятностное прогнозирование становится возможным при организации систематического контроля показателей надёжности. Ключевым является мониторинг вероятности безотказной работы P(t) для одного или группы однотипных объектов в течение заданного периода времени Tn.
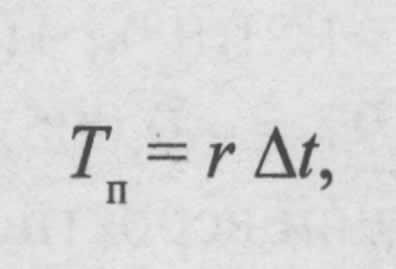
Процесс включает несколько этапов. Контроль осуществляется в течение r периодов, где Δt — это промежуток времени между последовательными проверками. Для каждого из этих периодов вычисляются значения вероятности безотказной работы: P(t1), P(t2) и так далее.
Анализ и моделирование данных
Полученный временной ряд значений P(t) затем подвергается аналитическому описанию. Для этого могут использоваться различные математические модели, например, аппроксимация многочленом или квадратичным полиномом, что позволяет выявить тренд и экстраполировать его на будущее.
Важным шагом в вероятностном прогнозировании является выбор обобщённого параметра. Из множества (k) контролируемых параметров системы выбирается один, который интегрально отражает изменение состояния всех остальных, что упрощает модель и делает прогноз более наглядным.
Практический пример
Рассмотрим наглядный пример из практики эксплуатации. Предположим, велось наблюдение за партией из 100 однотипных объектов, в ходе которого фиксировалось количество отказов n в определённые моменты времени.


На основе этих данных можно рассчитать значения вероятности безотказной работы для каждого контрольного интервала, построить график её изменения и, аппроксимировав полученную кривую, спрогнозировать значение надёжности на планируемый период эксплуатации.

