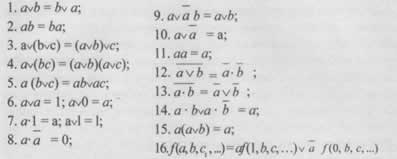Логико-вероятностные методы представляют собой мощный инструмент для оценки надежности сложных систем. Их суть заключается в том, чтобы сначала описать структуру и условия отказа системы на языке математической логики, а затем, используя аппарат теории вероятностей, вычислить количественные показатели надежности. Таким образом, задача расчета сводится к установлению связи между отказом всей системы (сложное событие) и отказами или работоспособностью ее отдельных компонентов (простые события).
Математический аппарат: алгебра высказываний
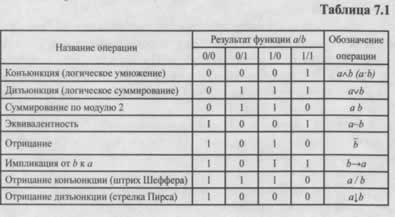
В основе этих методов лежат операции с событиями и высказываниями, которые изучаются в разделе математической логики — алгебре высказываний. В этом контексте под высказыванием понимается утверждение, которое может быть либо истинным (обозначается «1»), либо ложным («0»). При анализе надежности истинность часто соответствует работоспособности элемента, а ложность — его отказу. Высказывания бывают простыми (например, «элемент А исправен») и сложными, которые образуются из простых с помощью логических операций. Каждая операция строго определяет, при каких условиях истинности простых высказываний сложное высказывание будет истинным.
Алгоритм построения логической функции работоспособности
Для перехода от описания системы к логической функции, выражающей ее работоспособность через состояния элементов, рекомендуется следующий алгоритм:
1. На основе структурной схемы или таблицы истинности определить все комбинации состояний элементов (наборы простых высказываний), при которых система остается работоспособной (сложное высказывание истинно).
2. Для каждого такого набора записать конъюнкцию (логическое «И») простых высказываний: работоспособные элементы записываются как есть, а отказавшие — с операцией отрицания (логическое «НЕ»).
3. Все полученные конъюнкции объединить операцией дизъюнкции (логическое «ИЛИ»). Результатом будет логическая функция работоспособности (или, наоборот, отказа) системы.
Упрощение логических выражений
Для облегчения последующих вероятностных расчетов полученную логическую функцию часто необходимо упростить. Для этого используются законы и тождества алгебры логики (коммутативности, ассоциативности, дистрибутивности, де Моргана и др.). Цель упрощения — привести функцию к минимальной бесповторной форме, которая содержит наименьшее возможное количество операций и в которой каждый аргумент (состояние элемента) встречается только один раз. Это значительно упрощает подстановку вероятностных значений и конечные вычисления.