Параллельно-последовательные структуры служат ключевым инструментом для анализа и количественной оценки надежности сложных технических систем. Такой подход позволяет установить прямую зависимость между надежностью всей системы в целом и надежностью ее отдельных компонентов. Процесс расчета выполняется поэтапно: начинается с анализа простейших, элементарных узлов и постепенно переходит к более сложным конфигурациям. В основе метода лежит последовательное упрощение схемы путем замены групп параллельно или последовательно соединенных элементов на эквивалентные по надежности блоки.
Пример структурного анализа
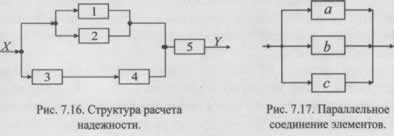
Рассмотрим практическое применение метода. Например, на рисунке 7.16 узел, объединяющий элементы 1 и 2, является элементарным. Более сложный узел формируется элементами 1, 2, 3 и 4. Вся эта структура может быть преобразована в эквивалентную, состоящую из одного обобщенного узла (1-2-3-4) и элемента 5, соединенных между собой последовательно. Такое преобразование существенно упрощает дальнейшие вычисления.
Расчет надежности при параллельном соединении
Перейдем к формулам для расчета. Рассмотрим параллельное соединение, состоящее из трех элементов (рис. 7.17). Критический отказ такого соединения наступает только в случае выхода из строя всех его элементов. Иными словами, система остается работоспособной, если функционирует хотя бы один из элементов: a, b или c, или любая их комбинация. Это условие можно формально описать с помощью функции алгебры логики (ФАЛ), где переменные a, b, c обозначают события, соответствующие работоспособному состоянию каждого элемента.
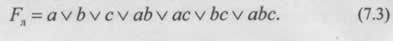
Функцию, которая связывает состояния элементов с состоянием системы, называют функцией работоспособности системы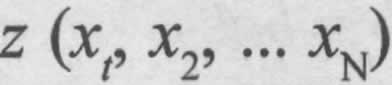 
. Для системного анализа вводятся два важных понятия:
1. Кратчайший путь успешного функционирования — это минимальная комбинация (конъюнкция) элементов, удаление любого из которых делает систему неработоспособной.
2. Минимальное сечение отказов — это минимальная комбинация отказов элементов (конъюнкция их отрицаний), при которой система гарантированно выходит из строя.
Используя эти понятия, условие работоспособности системы можно записать в одной из двух стандартных форм:
— Как дизъюнкцию всех кратчайших путей (дизъюнктивная нормальная форма, ДНФ).
— Как конъюнкцию отрицаний всех минимальных сечений (конъюнктивная нормальная форма, КНФ).
Переход к вероятностным оценкам
После того как функция работоспособности системы записана в виде ДНФ или КНФ, необходимо перейти к вероятностной функции для расчета количественных характеристик надежности (например, вероятности безотказной работы). Однако прямой переход невозможен, если одни и те же переменные входят в несколько логических конъюнкций (как в выражении 7.3), так как это приведет к некорректному учету зависимых событий. Поэтому выражение необходимо преобразовать к так называемой бесповторной форме функции алгебры логики (БФАЛ), где каждая переменная встречается только один раз.
Для такого преобразования разработан ряд эффективных алгоритмов, среди которых наиболее известны алгоритмы С.В. Макарова, Ю.Б. Мерекина, И.А. Рябинина, А.С. Смирнова и других ученых.
В качестве примера выполним минимизацию выражения (7.3):
