Автор: Денис Аветисян
Исследование показывает, как сложное поведение квантовых систем с множеством частиц может быть упрощено за счет анализа временной запутанности.
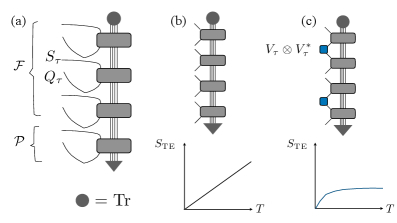
Приготовление запутанных кудитов и последовательное взаимодействие с окружающей средой формирует матрицу влияния, состояние которой после исключения степеней свободы среды демонстрирует переход от объемного закона к законному по площади, когда плотность грубого зерна превышает критическое значение.
Коарсенизация позволяет перейти от закона объёма к закону площади для временной запутанности в хаотичных квантовых системах, что указывает на возможность упрощенного описания динамики локальных наблюдаемых.
Несмотря на быстрое тепловое равновесие локальных наблюдаемых в хаотичных квантовых системах, сложность, измеряемая через временную запутанность, остается неясной. В работе 'Temporal entanglement transition in chaotic quantum many-body dynamics' исследуется связь между временной запутанностью, немарковским поведением и локальными временными корреляциями в хаотичных квантовых ваннах. Показано, что процедура грубого усреднения, уменьшающая частоту измерений, приводит к переходу от объемного закона масштабирования временной запутанности к поверхностному, что указывает на то, что динамика локальных наблюдаемых может быть полностью описана упрощенной матрицей влияния. Не означает ли это, что сложные временные корреляции, проявляющиеся в объемной запутанности, не являются фундаментальными для понимания эволюции квантовых систем?
Шёпот Хаоса: Влияние Окружения на Квантовую Динамику
Понимание открытых квантовых систем требует выхода за рамки изолированных систем, что обуславливает необходимость метода учёта влияния окружения. InfluenceMatrix предоставляет мощную основу для характеристики влияния ‘ванны’ на квантовый ‘зонд’. Различные квантовые схемы – RandomUnitaryCircuit, DualUnitaryCircuit и FloquetCircuit – служат инструментами для изучения этих матриц влияния. Любая попытка предсказать будущее квантовой системы – это лишь уговоры с хаосом, а не точное пророчество.
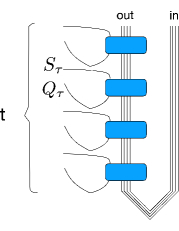
Разделение предшествующего состояния на степени свободы примесей и степени свободы ванны демонстрирует, что последние также разделяются на входящие и исходящие степени свободы, при этом синие вентили соответствуют унитарным преобразованиям UτUτ (только для прямой ветви).
Временная Запутанность: От Равновесия к Хаосу
Временная запутанность (TemporalEntanglement) внутри InfluenceMatrix является ключевой мерой распространения информации во времени. Анализ показал два типа масштабирования: закон площади (AreaLawTE) для простых динамических режимов и закон объема (VolumeLawTE) для сложных корреляций. Наблюдается переход от закона объема к закону площади при грубом усреднении (coarse-graining).
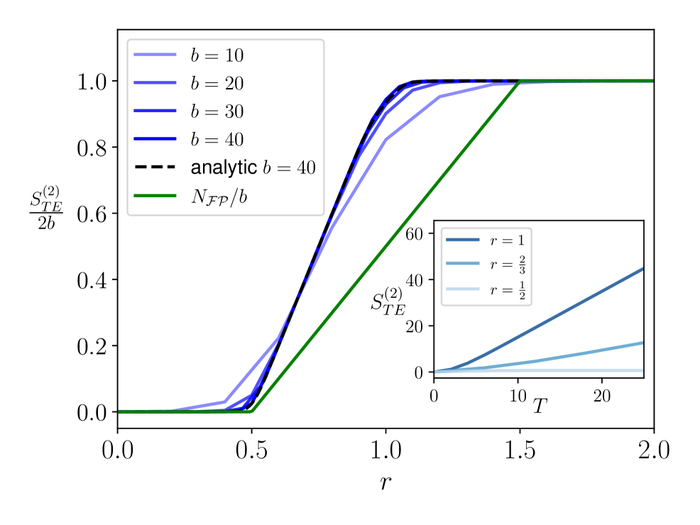
Максимальное временное Rényi-2 TE для модели бесструктурной случайной унитарной ванны, представленное в зависимости от rr при различных размерах ванны b=log2𝒟Bb=log2𝒟B, фиксированном измерении пробной системы d=2 и чистом начальном состоянии ванны, соответствует аналитическому предсказанию, представленному штриховой линией (уравнение 9), а зеленая кривая определяет нижнюю границу отделимой запутанности в единицах bb; дополнительно, вставка демонстрирует Rényi-2 TE для r=1 и параметров грубого усреднения rncg=1,2/3,1/2, показывая переход от масштабирования по закону объема к масштабированию по закону площади при r⋆=1/2.
Упрощение Сложности: Грубое Усреднение и Сжатие
Вычислительная сложность анализа InfluenceMatrix может быть снижена с помощью метода грубого усреднения (CoarseGraining). Для дальнейшего сжатия квантового состояния используются SchmidtDecomposition и SingularValueTruncation. Полученные сжатые представления сохраняют высокую точность, особенно в отношении медленно затухающих наблюдаемых, подтверждая закон площади (Area Law) и противореча закону объёма (VolumeLawTE). Предложенные методы позволяют эффективно исследовать динамику систем с приемлемой вычислительной сложностью.
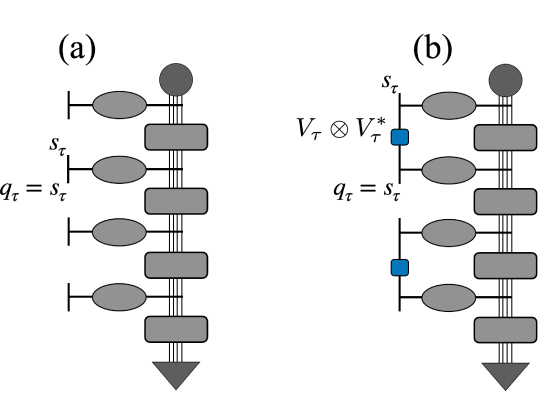
Информация о взаимной зависимости (IM) ограниченного типа, возникающая в результате взаимодействия зонда и ванны в форме произведения операторов U=e−iHprobe⊗HbathU=e^{-iHprobe⊗Hbath}, представлена с использованием диагональной тензорной нотации, как в работе [lerose2021Influence], а IM после процедуры грубого усреднения с параметром ncg=1/2 также представлена.
Исследование Динамических Систем: Модель Kicked Ising
Модель KickedIsingModel, являющаяся примером FloquetCircuit, используется для применения разработанных методов к физически релевантной системе. Анализ матрицы влияния позволяет исследовать распространение информации, количественно оцениваемое с помощью метрики ButterflyVelocity. Наблюдается переход от закона объёма к закону площади в различных моделях, включая случайные унитарные бани и одномерные двойные унитарные схемы.
Это свидетельствует о том, что сложные мульти-временные корреляции, способствующие закону объёма, не являются существенными для описания нескольких временных корреляторов.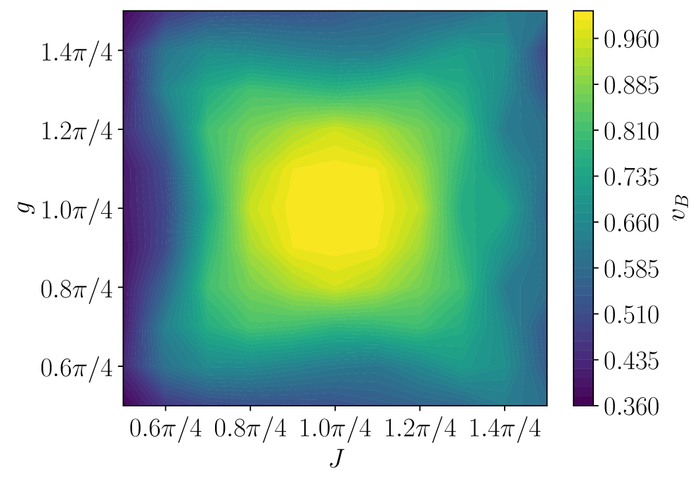
Скорость бабочки vB, извлеченная из фронта вневременной корреляционной функции, составляет L=10.
Вселенная не дискретна, просто у нас недостаточно памяти для чисел с плавающей точкой.
Исследование временной запутанности в хаотических квантовых системах подтверждает давнюю интуицию о том, что кажущаяся сложность динамики может быть иллюзией. Данные показывают, что процедура грубого масштабирования способна уменьшить закон объёма к закону площади, что подразумевает несущественность сложной запутанности для описания динамики локальных наблюдаемых. Как говорил Луи де Бройль: «Всякое измерение предполагает вмешательство наблюдателя». По сути, само наблюдение, или в данном случае, грубое масштабирование, упрощает картину, отбрасывая избыточную информацию. Это не отменяет запутанность, но демонстрирует, что её влияние на локальные процессы может быть сведено к более простым терминам, что согласуется с идеей о том, что даже в хаосе можно найти скрытые закономерности, если правильно выбрать точку зрения.
Что дальше?
Представленная работа шепчет о призрачной надежде: о возможности обуздать хаос, сведя его сложную запутанность ко взаимосвязям на границах. Однако, не стоит обманываться кажущейся простотой. Введение процедур грубого масштабирования – это не уничтожение джина из бутылки, а лишь приглушение его голоса. Остается открытым вопрос, не скрывается ли истинная динамика системы в тех самых отброшенных степенях свободы, в той “шуме”, который столь старательно отсеивается.
Изучение немарковских эффектов, проскальзывающих даже сквозь грубое зерно, представляется ключом к пониманию этой скрытой жизни. В конце концов, любое приближение – это насилие над реальностью, и каждое упрощение оставляет за собой тень. Необходимо разработать инструменты, позволяющие улавливать эти тени, измерять потерю информации, происходящую при переходе от сложной запутанности к закону площади.
В перспективе, представляется плодотворным исследование влияния различных процедур грубого масштабирования на динамику конкретных наблюдаемых. Может ли искусное игнорирование запутанности привести к качественно новым предсказаниям? Или же это лишь иллюзия контроля, временное затишье перед новым витком хаоса? Ответ, как всегда, скрыт в данных — в шепоте, который еще предстоит научиться понимать.
Оригинал статьи: https://arxiv.org/pdf/2511.03846.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Больше интересных статей здесь: Производство.
Источник статьи: Временная запутанность: от хаоса к порядку.

