Биномиальное распределение: модель для серии испытаний
Рассмотрим ситуацию, когда проводится серия из N независимых испытаний или наблюдается N однотипных объектов. В каждом отдельном испытании интересующее нас событие A (например, отказ элемента) может произойти с постоянной вероятностью p. Вероятность того, что событие не произойдет, обозначается как q = 1 - p. Количество успехов (появлений события A) в такой серии является дискретной случайной величиной, которая описывается биномиальным законом распределения.
Согласно этому закону, вероятность того, что событие A наступит ровно n раз в N испытаниях, вычисляется по формуле:
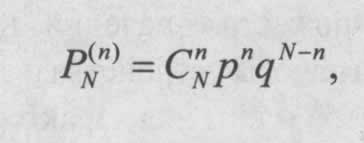
Здесь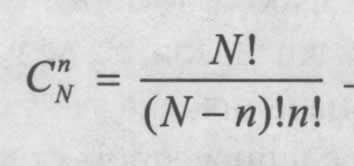 
— это биномиальный коэффициент, равный количеству сочетаний из N элементов по n, который определяет число различных способов получить n успехов.
Для биномиально распределенной величины важными числовыми характеристиками являются:
- Математическое ожидание M(n) — среднее ожидаемое количество успехов.
- Дисперсия D(n) — мера разброса значений вокруг среднего.
- Среднеквадратическое отклонение σ(n) — корень из дисперсии, имеющий ту же размерность, что и сама величина.
Эти характеристики рассчитываются по следующим формулам:
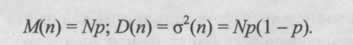
На практике часто возникает вопрос о вероятности хотя бы одного появления события A в серии испытаний. Эту вероятность удобно находить через противоположное событие (ни одного успеха):
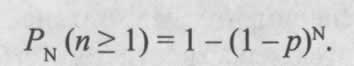
Распределение Пуассона: модель для редких событий и потоков отказов
Распределение Пуассона занимает особое место в теории надежности, так как оно эффективно моделирует возникновение случайных отказов в сложных технических системах. Оно описывает вероятность появления определенного числа событий за фиксированный интервал времени, при условии, что эти события происходят независимо и с постоянной средней интенсивностью.
Это распределение тесно связано с понятием потока событий (например, потока отказов или восстановлений). Поток событий называется пуассоновским, если он удовлетворяет трем фундаментальным требованиям:
- Стационарность: Вероятность возникновения k событий на любом промежутке времени зависит только от длины этого промежутка, а не от его положения на временной оси. Это означает постоянную среднюю плотность событий во времени.
- Ординарность: События происходят поодиночке. Вероятность одновременного появления двух или более событий в бесконечно малый момент времени пренебрежимо мала.
- Отсутствие последействия: Вероятность наступления событий в будущем промежутке времени не зависит от того, что происходило в прошлом. События являются независимыми.
Вероятность того, что в пуассоновском потоке с интенсивностью λ за время t произойдет ровно k событий, задается формулой:
Для пуассоновского распределения математическое ожидание (среднее число событий) и дисперсия численно равны и рассчитываются как:
