Процесс определения необходимого количества запасных частей (ЗЧ) для радиоэлектронного оборудования (РЭО) и систем автоматики (СА) строится на принципе поддержания их работоспособности в течение заданного срока с требуемой вероятностью. Основная задача такого расчета — найти оптимальный комплект запасных частей (ЗИП), который минимизирует затраты (по объему, массе или стоимости) при обеспечении заданных показателей надежности. Альтернативный подход — при заданных ограничениях по ресурсам определить максимально достижимую вероятность безотказной работы системы.
Влияние запаса частей на надежность системы
Поскольку РЭО и СА являются системами многократного действия, их работоспособность напрямую зависит от наличия запасных элементов. Ключевой задачей становится установление количественной связи между вероятностью P(t) успешного выполнения системой своих функций за время t и количеством запасных частей z. Эта зависимость позволяет не только оценить влияние комплекта ЗИП на общую надежность, но и рассчитать минимально необходимое число запасных элементов, гарантирующее работу объекта с заданной вероятностью Pz(t).
Критерии расчета: от простоев до вероятности отказов
Один из распространенных критериев при планировании ЗИП — среднее время вынужденного простоя прибора из-за отсутствия нужной запасной части. Фактически, ситуация, когда в комплекте нет элемента для замены отказавшего в системе, приравнивается к отказу самого комплекта ЗИП.
Рассмотрим систему, состоящую из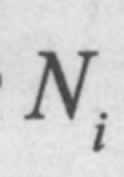 
элементов i-го типа (где i = 1, 2, ... m), соединенных последовательно с точки зрения надежности. Если отказы элементов подчиняются экспоненциальному закону как в рабочем режиме, так и в режиме ожидания (хранения), то среднее ожидаемое количество отказов за расчетное время 
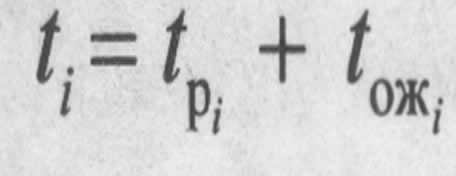можно выразить формулой:
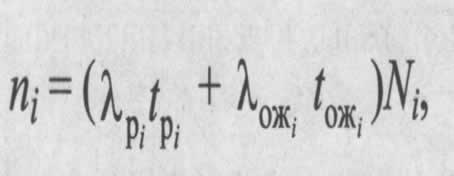
Здесь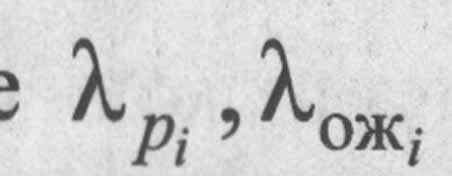 
— интенсивности отказов элементов i-го типа в рабочем режиме и режиме ожидания; 
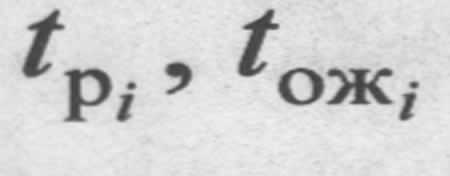— соответственно, время работы и время ожидания элемента.
Модель расхода запасных частей и вероятность безотказной работы
Предположим, что в электрической системе каждый отказавший элемент немедленно заменяется новым из комплекта ЗИП (без восстановления старого). В этом случае количество израсходованных запасных частей 
будет равно числу отказов n, произошедших за то же время:
где 
— это количество запасных частей i-го типа в комплекте.
Если в ЗИП вообще нет запасных частей данного типа (
), формула (8.1) описывает классическую вероятность безотказной работы системы с экспоненциальным законом распределения отказов:
Вероятность же того, что система из элементов i-го типа успешно проработает время t, то есть что запасных частей этого типа хватит, определяется как сумма вероятностей:
Практическое использование номограмм и выбор уровня обеспеченности
Функцию 
для нахождения необходимого количества запасных частей 
в зависимости от параметра 
удобно представлять в виде номограммы (рис. 8.1).
Анализ номограммы показывает важный практический вывод: если количество запасных частей 
просто равно среднему ожидаемому числу отказов 
, то вероятность отсутствия простоев системы из-за нехватки ЗЧ при n > 1 лишь ненамного превышает 0.50. Такой уровень надежности явно недостаточен для стабильной работы. Это объясняется статистической природой отказов: фактическое их число за расчетный период с примерно равной вероятностью может оказаться как меньше, так и больше среднего ожидаемого значения 
.
Поэтому вероятность достаточности запасных частей i-го типа в ЗИП рассчитывают, исходя из общей заданной вероятности 
того, что всего комплекта ЗИП хватит для поддержания работоспособности системы в целом. Для особо ответственных устройств требуемые значения вероятности Pz(t) выполнения системой своих функций при наличии z запасных частей задаются очень высокими.
